
【题目】如图,已知![]() ,现将一直角三角形
,现将一直角三角形![]() 放入图中,其中
放入图中,其中![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
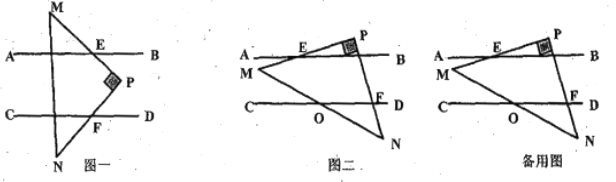
(1)当![]() 所放位置如图一所示时,则
所放位置如图一所示时,则![]() 与
与![]() 的数量关系为 ;
的数量关系为 ;
(2)当![]() 所放位置如图二所示时,试说明:
所放位置如图二所示时,试说明:![]() ;
;
(3)在(2)的条件下,若![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)![]() ;(2)详见解析;(3)45°
;(2)详见解析;(3)45°
【解析】
(1)由平行线性质得出∠1=∠PFD,∠2=∠AEM,据此进一步求解即可;
(2)由平行线性质可得∠PFD+∠BHF=180°,再根据角的互余关系进一步证明即可;
(3)根据角的互余关系得出∠PHE,再根据平行线性质得出∠PFC度数,然后根据三角形外角性质进一步求解即可.
(1)如图所示,作PG∥AB,则PG∥CD,
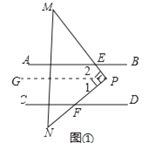
∴∠1=∠PFD,∠2=∠AEM,
∵∠1+∠2=∠P=90°,
∴![]() ,
,
故答案为:![]() ;
;
(2)如图所示,
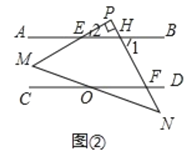
∵AB∥CD,
∴∠PFD+∠BHF=180°,
∵∠P=90°,
∴∠BHF+∠PEB=90°,
∵∠PEB=∠AEM,
∴∠BHF=∠PHE=90°∠AEM,
∴∠PFD+90°∠AEM=180°,
∴∠PFD∠AEM=90°
(3)如图所示,
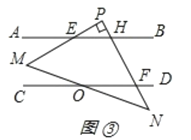
∵∠P=90°,
∴∠PHE=90°∠FEB=75°,
∵AB∥CD,
∴∠PFC=∠PHE=75°,
∵∠PFC=∠N+∠DON,
∴∠N=75°30°=45°.


科目:初中数学 来源: 题型:
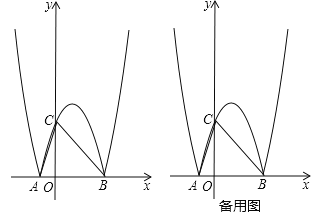
【题目】(2017江苏省宿迁市,第25题,10分)如图,在平面直角坐标系xOy中,抛物线![]() 交x轴于A,B两点(点A在点B的左侧),将该抛物线位于x轴上方曲线记作M,将该抛物线位于x轴下方部分沿x轴翻折,翻折后所得曲线记作N,曲线N交y轴于点C,连接AC、BC.
交x轴于A,B两点(点A在点B的左侧),将该抛物线位于x轴上方曲线记作M,将该抛物线位于x轴下方部分沿x轴翻折,翻折后所得曲线记作N,曲线N交y轴于点C,连接AC、BC.
(1)求曲线N所在抛物线相应的函数表达式;
(2)求△ABC外接圆的半径;
(3)点P为曲线M或曲线N上的一动点,点Q为x轴上的一个动点,若以点B,C,P,Q为顶点的四边形是平行四边形,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
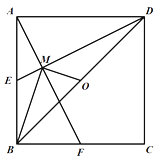
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=![]() MF.其中正确结论的是( )
MF.其中正确结论的是( )
A. ①③④ B. ②④⑤ C. ①③④⑤ D. ①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在Rt△ABC中,∠ACB=90°,AC=4,BC=2,D是AC边上的一个动点,将△ABD沿BD所在直线折叠,使点A落在点P处.
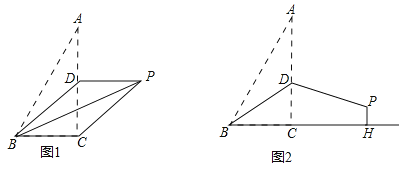
(1)如图1,若点D是AC中点,连接PC.
①写出BP,BD的长;
②求证:四边形BCPD是平行四边形.
(2)如图2,若BD=AD,过点P作PH⊥BC交BC的延长线于点H,求PH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵ ,(已知)
∴∠AGD= (等式性质)

查看答案和解析>>
科目:初中数学 来源: 题型:
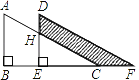
【题目】如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分面积是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运输部门规定:办理托运,当一种物品的重量不超过16千克时,需付基础费30元和保险费a元:为限制过重物品的托运,当一件物品超过16千克时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某件物品的重量为x千克.
(1)当x≤16时,支付费用为__________________元(用含a的代数式表示);
当x≥16时,支付费用为_________________元(用含x和a、b的代数式表示);
(2)甲、乙两人各托运一件物品,物品重量和支付费用如下表所示
物品重量(千克) | 支付费用(元) |
18 | 39 |
25 | 53 |
试根据以上提供的信息确定a,b的值.
(3)根据这个规定,若丙要托运一件超过16千克的物品,但支付的费用不想超过70元,那么丙托运的物品最多是多少千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
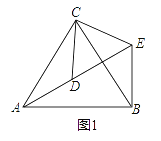
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
(3)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(Ⅰ)请求出∠AEB的度数;(Ⅱ)判断线段CM、AE、BE之间的数量关系,并说明理由.
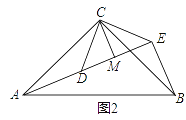
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算a![]() b=a(1-b),下面给出了关于这种运算的四个结论:
b=a(1-b),下面给出了关于这种运算的四个结论:
①2![]() (-2)=6 ②a
(-2)=6 ②a![]() b=b
b=b![]() a
a
③若a+b=0,则(a![]() a)+(b
a)+(b![]() b)=2ab ④若a
b)=2ab ④若a![]() b=0,则a=0.
b=0,则a=0.
其中正确结论的序号是 (填上你认为所有正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com