
分析 (1)先确定出DF,然后用勾股定理即可求出圆的半径,即可得出结论;
(2)①令y=0解出x的只即可;②由切线得出PN=2,再用勾股定理得出AN,用锐角三角函数即可得出k的值,③判断出直线l与⊙相切时和相交时,两种情况讨论计算.
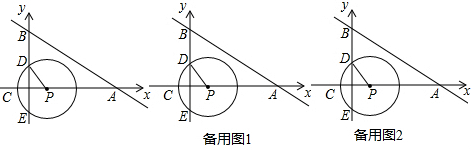
解答 解:(1)如图1,∵C(-1,0),
∴OC=1,
∵DE=2$\sqrt{3}$,
∴DF=$\frac{1}{2}$DE=$\sqrt{3}$,
∴PF=PC-OC=PD-1,
根据勾股定理得,DP2-PF2=DF2,
∴DP2-(DP-1)2=3,
∴DP=2,
∴OP=1,
∴P(0,1),
(2)①令y=0,则k(x-5)=0,
∵k≠0,
∴x=5,
∴A(5,0),
故答案为:(5,0);
②如图1,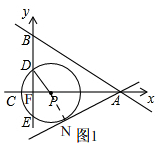 过点P作PN⊥AN于N,
过点P作PN⊥AN于N,
由①知,A(5,0),
∴OA=5,
∴PA=4,
∵直线l与⊙P的相切,
∴PN=PD=2
,根据勾股定理得,AN=$\sqrt{A{P}^{2}-P{N}^{2}}$=2$\sqrt{3}$,
∴tan∠PAN=$\frac{PN}{AN}$=$\frac{\sqrt{3}}{3}$,
∴k=±$\frac{\sqrt{3}}{3}$,
③∵C(-1,0),D(0,$\sqrt{3}$),
∴CD=2,
∵DP=2,
∴∠CPD=60°,
∵在y轴右侧的直线l上只存在一个点M,使∠DMC=30°,
∴点M在⊙P上,即:直线l与⊙P相切或与⊙P相交,且一个交点在y轴左侧;
Ⅰ,直线l与⊙P相切时,k=±$\frac{\sqrt{3}}{3}$,
Ⅱ,直线l与⊙P相交,且一个交点在y轴左侧时,k=tan∠DAC=$\frac{DF}{AF}$=$\frac{\sqrt{3}}{5}$,
∴-$\frac{\sqrt{3}}{5}$≤k≤$\frac{\sqrt{3}}{5}$,
即:k的取值范围为:-$\frac{\sqrt{3}}{5}$≤k≤$\frac{\sqrt{3}}{5}$,或k=±$\frac{\sqrt{3}}{3}$.
点评 此题是圆的综合题,主要考查了圆的性质,切线的性质,直线和圆相交的特点,锐角三角函数,解本题的关键是理解直线与x轴的夹角的正切值是此直线的斜率k的绝对值,是一道比较简单的中考常考题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
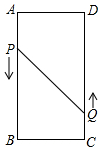 如图,A、B、C、D为矩形的四个顶点,AB=6cm,AD=2cm,动点P、Q分别从点A、C同时出发,点P以2cm/s的速度向终点B移动,点Q以1cm/s的速度向终点D移动,当有一点到达终点时,另一点也停止运动.设运动时间为t 求:
如图,A、B、C、D为矩形的四个顶点,AB=6cm,AD=2cm,动点P、Q分别从点A、C同时出发,点P以2cm/s的速度向终点B移动,点Q以1cm/s的速度向终点D移动,当有一点到达终点时,另一点也停止运动.设运动时间为t 求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
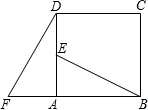 如图,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF=AB,已知△ABE≌△ADF.
如图,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF=AB,已知△ABE≌△ADF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
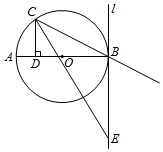 如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB于D,AD=2,CD=4.∠BCD的角平分线CE与过点B的切线l交过点E.
如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB于D,AD=2,CD=4.∠BCD的角平分线CE与过点B的切线l交过点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
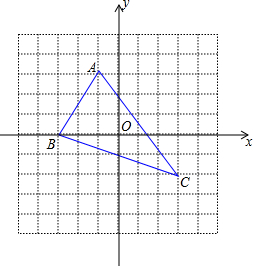 如图,在正方形网格中,△ABC的各顶点的坐标是A(-1,3)、B(-3,0)、C(3,-2),有一个△A′B′C′与△ABC关于x轴对称.
如图,在正方形网格中,△ABC的各顶点的坐标是A(-1,3)、B(-3,0)、C(3,-2),有一个△A′B′C′与△ABC关于x轴对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com