
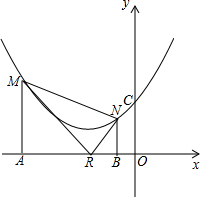
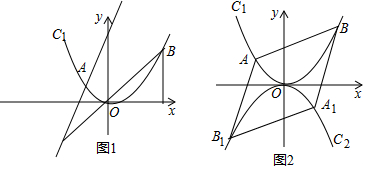
 抛物线y=$\frac{1}{4}$x2+x+n-1的顶点在直线y=x+3上.过点(-2.2)的直线交该抛物线于点M.N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B
抛物线y=$\frac{1}{4}$x2+x+n-1的顶点在直线y=x+3上.过点(-2.2)的直线交该抛物线于点M.N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B分析 (1)利用配方法求出抛物线顶点坐标,利用待定系数法即可解决问题.
(2)首先利用两点间距离公式证明MA=MG,同理可得NG=NB,再证明△MAR∽△NBR,推出∠ARM=∠NRB,由∠GRA=∠GRB=90°,推出∠MRG=∠NRG,由GR∥OC,推出∠GRN=∠RCO,可得∠MRN=2∠RCO.
(3)如图3中,$\frac{1}{AM}$+$\frac{1}{BN}$的值是定值.连接BM交GR于K,连接AK,KN.首先证明A、K、N共线,由AM∥GR∥BN,推出$\frac{GK}{AM}$=$\frac{GN}{NM}$=$\frac{RB}{AB}$=$\frac{RK}{AM}$,推出GK=RK=1,由$\frac{KR}{AM}$=$\frac{RB}{AB}$,$\frac{RK}{NB}$=$\frac{AR}{AB}$,推出$\frac{KR}{AM}$+$\frac{RK}{NB}$=$\frac{RB}{AB}$+$\frac{AR}{AB}$=$\frac{AB}{AB}$=1,推出$\frac{1}{AM}$+$\frac{1}{BN}$=$\frac{1}{KR}$=1即可解决问题.
解答 解:(1)∵y=$\frac{1}{4}$x2+x+n-1=$\frac{1}{4}$(x+2)2+n-2,
∴抛物线的顶点坐标为(-2,n-2),
∵抛物线y=$\frac{1}{4}$2+x+n-1的顶点在直线y=x+3上,
∴n-2=-2+3,
∴n=3.
(2)设M(m,$\frac{1}{4}$m2+m+2),G(-2,2),
∴MG=$\sqrt{(m+2)^{2}+(\frac{1}{4}{m}^{2}+m)^{2}}$
=$\sqrt{\frac{1}{16}{m}^{2}+2•\frac{1}{4}{m}^{2}(m+2)+(m+2)^{2}}$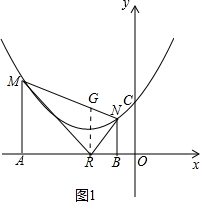
=$\sqrt{(\frac{1}{4}{m}^{2}+m+2)^{2}}$
=$\frac{1}{4}$m2+m+2,
∴MA⊥x轴,
∴AM=$\frac{1}{4}$m2+m+2,同理可证NG=NB,
∵R(-2,0),G(-2,2),BN⊥OR,
∴AM∥GR∥BN,
∴$\frac{GM}{GN}$=$\frac{AR}{RB}$,
∴$\frac{AM}{BN}$=$\frac{AR}{BR}$,
∵∠MAR=∠RBN,
∴△MAR∽△NBR,
∴∠ARM=∠NRB,
∵∠GRA=∠GRB=90°,
∴∠MRG=∠NRG,
∵GR∥OC,
∴∠GRN=∠RCO,
∴∠MRN=2∠RCO.
(3)如图3中,$\frac{1}{AM}$+$\frac{1}{BN}$的值是定值.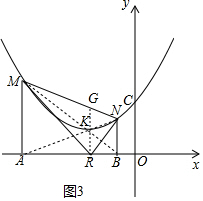
连接BM交GR于K,连接AK,KN.
∵GK∥BN,
∴$\frac{MG}{GN}$=$\frac{MK}{KB}$,∵MA=MG,NG=NB,
∴$\frac{AM}{BN}$=$\frac{MK}{KB}$,
∵AM∥BN,
∴∠AMK=∠NBK,
∴△AMK∽△NBK,
∴∠AKM=∠NKB,
∵∠NKB+∠MKN=180°,
∴∠AKM+∠MKN=180°,
∴A、K、N共线,
∵AM∥GR∥BN,
∴$\frac{GK}{AM}$=$\frac{GN}{NM}$=$\frac{RB}{AB}$=$\frac{RK}{AM}$,
∴GK=RK=1,
∵$\frac{KR}{AM}$=$\frac{RB}{AB}$,$\frac{RK}{NB}$=$\frac{AR}{AB}$,
∴$\frac{KR}{AM}$+$\frac{RK}{NB}$=$\frac{RB}{AB}$+$\frac{AR}{AB}$=$\frac{AB}{AB}$=1,
∴$\frac{1}{AM}$+$\frac{1}{BN}$=$\frac{1}{KR}$=1.
∴$\frac{1}{AM}$+$\frac{1}{BN}$的值是定值,
∴$\frac{1}{AM}$+$\frac{1}{BN}$=1.
点评 本题考查二次函数综合题、两点间距离公式、平行线分线段成比例定理、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用平行线分线段成比例定理,解决线段之间的关系问题,属于中考压轴题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
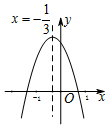 如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:
如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
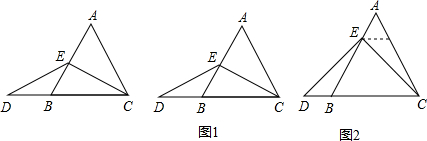
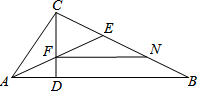 如图,在△ABC中,CD⊥AB,且CD2=AD•DB,AE平分∠CAB交CD于F,∠EAB=∠B,CN=BE.①CF=BN;②∠ACB=90°;③FN∥AB;④AD2=DF•DC.则下列结论正确的是①②③④.
如图,在△ABC中,CD⊥AB,且CD2=AD•DB,AE平分∠CAB交CD于F,∠EAB=∠B,CN=BE.①CF=BN;②∠ACB=90°;③FN∥AB;④AD2=DF•DC.则下列结论正确的是①②③④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com