
分析 直接利用绝对值的性质得出:|x+l|+|x-2|≥3,|y-2|+|y+1|≥3,|z-3|+|z+l|≥4,进而利用已知得出答案.
解答 解:∵|x+l|+|x-2|≥3,
|y-2|+|y+1|≥3,
|z-3|+|z+l|≥4,
∴(|x+l|+|x-2|)(|y-2|+|y+1|)(|z-3|+|z+l|)≥36,
∵(|x+l|+|x-2|)(|y-2|+|y+1|)(|z-3|+|z+l|)=36,
∴|x+l|+|x-2|=3,|y-2|+|y+1|=3,|z-3|+|z+l|=4,
∴-1≤x≤2,-1≤y≤2,-1≤z≤3,
∴-5≤x+y-z≤5,
故最大值5,最小值-5.
点评 此题主要考查了绝对值,正确得出x,y,z的取值范围是解题关键.


科目:初中数学 来源: 题型:解答题
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 每人门票价 | 13元 | 11元 | 9元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
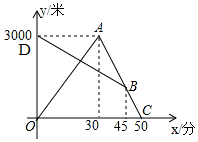 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com