
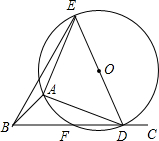 如图,∠ABC=45°,△ADE是等腰直角三角形,AE=AD,顶点A、D分别再∠ABC的两边BA、BC上滑动(不与点B重合),△ADE的外接圆交BC于点F,O为圆心.
如图,∠ABC=45°,△ADE是等腰直角三角形,AE=AD,顶点A、D分别再∠ABC的两边BA、BC上滑动(不与点B重合),△ADE的外接圆交BC于点F,O为圆心.分析 (1)根据等腰直角三角形的性质和圆周角定理即可得到结论;
(2)①根据已知条件得到AB=AF,∠BAF=90°推出△ABD≌△AFE,根据全等三角形的性质得到BD=EF,由线段的和差得到EF-DF=BD-DF=BF,根据三角函数的定义得到BF=$\sqrt{2}$AF,即可得到结论;
②由(2)①得BD=EF,根据已知条件得到BF=8,根据勾股定理得到8$\sqrt{2}$<BE≤4$\sqrt{13}$,求得8<EF<12,于是得到S=$\frac{π}{2}$(x-4)2+8π,根据二次函数的性质即可得到结论.
解答  解:(1)∠AFE=45°,连接AF,
解:(1)∠AFE=45°,连接AF,
∵△ADE是等腰直角三角形,
∴∠AFE=∠EDF=45°;
(2)①连接EF,
∵∠EFD=∠EAD=90°,
∴∠BFE=90°,
∵∠AFE=45°,
∴∠AFB=∠AFE=45°,
∴AB=AF,∠BAF=90°,
∴∠BAD=∠FAE,
在△ABD和△AFE中,
$\left\{\begin{array}{l}{AD=AE}\\{∠BAD=∠FAE}\\{AB=AF}\end{array}\right.$,
∴△ABD≌△AFE,
∴BD=EF,
∴EF-DF=BD-DF=BF,
∵AF=BF•cos∠AFB=$\frac{\sqrt{2}}{2}$BF,即BF=$\sqrt{2}$AF,
∴EF-DF=$\sqrt{2}$AF;
②由(2)①得BD=EF,
∵∠BAF=90°,AB=4$\sqrt{2}$,
∴BF=$\frac{AB}{cos∠ABF}$=$\frac{4\sqrt{2}}{cos45°}$=8,
设BD=x,则EF=x,DF=x-8,
∵BE2=EF2+BF2,8$\sqrt{2}$<BE≤4$\sqrt{13}$,
∴128<EF2+82<208,
∴8<EF<12,即8<x<12,
∴S=$\frac{π}{4}$DE2=$\frac{π}{4}$[x2+(x-8)2]=$\frac{π}{2}$(x-4)2+8π,
∵$\frac{π}{2}$>0,
∴抛物线的开口向上,
∵抛物线的对称轴为直线x=4,
∴当8<x≤12时,16π<S≤40π.
点评 本题考查了等腰直角三角形的性质,全等三角形的判定和性质,勾股定理,锐角三角函数,二次函数的性质,连接EF构造直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
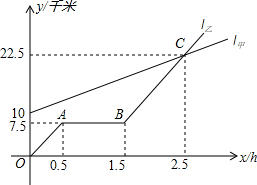 如图,l甲,l乙分别表示甲走路与乙骑自行车(在同一条路上)行走的路程y与时间x的关系,观察图象并回答下列问题:
如图,l甲,l乙分别表示甲走路与乙骑自行车(在同一条路上)行走的路程y与时间x的关系,观察图象并回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
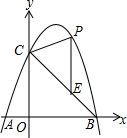 如图,在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象与y轴交于点C(0,8),与x轴交于A,B两点,其中A(-2,0),B(6,0).
如图,在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象与y轴交于点C(0,8),与x轴交于A,B两点,其中A(-2,0),B(6,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
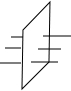 如图,有红、黄、蓝粗细均匀的木棍各一根分别穿过木板,甲乙两人在木板的两侧同时随机抓住一根木棍,则他们抓住的木棍颜色相同的概率是$\frac{1}{3}$.
如图,有红、黄、蓝粗细均匀的木棍各一根分别穿过木板,甲乙两人在木板的两侧同时随机抓住一根木棍,则他们抓住的木棍颜色相同的概率是$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
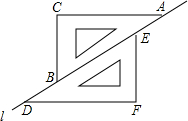 如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )| A. | BD=AE | B. | CB=BF | C. | BE⊥CF | D. | BA平分∠CBF |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com