
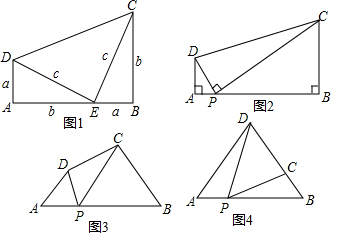
 如图1是美国第20届总统加菲尔德于1876年公开发表的勾股定理一个简明证法,聪明的思齐和他的社团小朋友们发现:两个直角三角形在发生变化过程中,只要满足一定的条件,就会有神奇的结果:
如图1是美国第20届总统加菲尔德于1876年公开发表的勾股定理一个简明证法,聪明的思齐和他的社团小朋友们发现:两个直角三角形在发生变化过程中,只要满足一定的条件,就会有神奇的结果:分析 (1)欲证明AD•BC=AP•BP,只要证明△ADP∽△BPC即可.
(2)结论不变.只要证明△ADP∽△BPC即可.
(3)如图4中,设经过t秒点D到AB的距离等于CD长,过点D作DE⊥AB于E.利用(2)的结论构建方程即可.
解答 解:(1)证明:如图2中,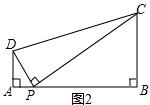
∵∠DPC=∠A=∠B=90°,
∴∠ADP+∠APD=90°,∠BPC+∠APD=90°,
∴∠ADP=∠BPC,
∴△ADP∽△BPC,
∴$\frac{AD}{BP}$=$\frac{AP}{BC}$,
∴AD•BC=AP•BP.
(2)结论AD•BC=AP•BP仍然成立.
理由:如图3中,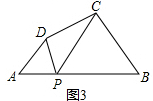
∵∠BPD=∠DPC+∠BPC,
又∵∠BPD=∠A+∠ADP,
∴∠DPC+∠BPC=∠A+∠ADO,
∵∠DPC=∠A=θ,
∴∠BPC=∠ADP,又∵∠A=∠B=θ,
∴△ADP∽△BPC,
∴$\frac{AD}{BP}$=$\frac{AP}{BC}$,
∴AD•BC=AP•BP.
(3)如图4中,设经过t秒点D到AB的距离等于CD长,过点D作DE⊥AB于E.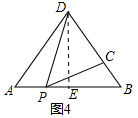
∵AD=BD=10,AB=12,
∴AE=BE=6,
在RT△ADE中,DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴DC=DE=8,
∴BC=10-8=2,
又∵AD=BD,
∴∠A=∠B,
∵∠DPC=∠A,
∴∠DPC=∠A=∠B,
由(2)可知AD•BC=AP•BP,
又AP=t,BP=12-t,
∴t(12-t)=10×2,
解得t=2或10,
∴t的值为2秒或10秒.
点评 本题考查相似综合题、相似三角形的判定和性质、勾股定理、直角三角形两锐角互余等知识,解题的关键是正确寻找相似三角形的条件,解题时注意图形发生变化,结论不变,证明方法完全类似,属于中考压轴题.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:选择题
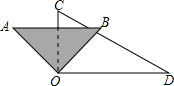 如图,将一副三角板的直角顶点重合在一起,将三角板AOB绕点O的旋转过程中,下列结论成立的是( )
如图,将一副三角板的直角顶点重合在一起,将三角板AOB绕点O的旋转过程中,下列结论成立的是( )| A. | ∠AOD>∠BOC | B. | ∠AOC≠∠BOD | C. | ∠AOD-∠BOC=45° | D. | ∠AOD+∠BOC=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
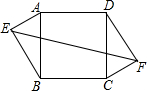 如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD外的点,且AE=FC=6,BE=DF=8,则EF的长为( )
如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD外的点,且AE=FC=6,BE=DF=8,则EF的长为( )| A. | 14 | B. | 16 | C. | $14\sqrt{2}$ | D. | $14\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,点E、F分别在边AD、BC上,且EF∥CD,G为边AD延长线上一点,连接BG,则图中与△ABG相似的三角形有( )个.
如图,在?ABCD中,点E、F分别在边AD、BC上,且EF∥CD,G为边AD延长线上一点,连接BG,则图中与△ABG相似的三角形有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com