
【题目】已知:△ABC是边长为3的等边三角形,以BC为底边作一个顶角为120等腰△BDC.点M、点N分别是AB边与AC边上的点,并且满足∠MDN=60.
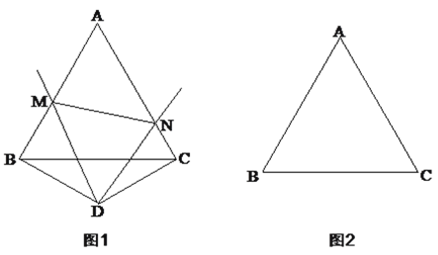
(1)如图1,当点D在△ABC外部时,求证:BM+CN=MN;
(2)在(1)的条件下求△AMN的周长;
(3)当点D在△ABC内部时,其它条件不变,请在图2中补全图形,并直接写出△AMN的周长.
【答案】(1)证明见解析;(2)6;(3)3.
【解析】试题分析:(1)延长AB至F,使BF=CN,连接DF,只要证明△BDF≌△CND,△DMN≌△DMF即可解决问题;
(2)利用(1)中结论即可解决问题;
(3)延长BD交AC于P,CD于Q,令KP=QM,交AC于P,连接DK.通过证明△BDQ≌△CDP,△MDQ≌△PDK,△MDN≌△KDN证得△AMN的周长=![]() (AB+AC)=3.
(AB+AC)=3.
试题解析:(1)延长AB至F,使BF=CN,连接DF,
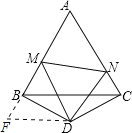
∵△BDC是等腰三角形,且∠BDC=120°
∴∠BCD=∠DBC=30°
∵△ABC是边长为3的等边三角形
∴∠ABC=∠BAC=∠BCA=60°
∴∠DBA=∠DCA=90°
在Rt△BDF和Rt△CND中,
∵BF=CN,DB=DC
∴△BDF≌△CND
∴∠BDF=∠CDN,DF=DN
∵∠MDN=60°
∴∠BDM+∠CDN=60°
∴∠BDM+∠BDF=60°,∠FDM=60°=∠MDN,DM为公共边
∴△DMN≌△DMF,
∴MN=MF,
∵MF=BM+BF=MN+CN,
∴MN=BM+CN.
(2)∵MN=BM+CN,
∴△AMN的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=6.
(3)延长BD交AC于P,CD于Q,令KP=QM,交AC于P,连接DK.
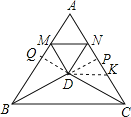
∵△BDC是等腰三角形,且∠BDC=120°
∴BD=CD,∠DBC=∠DCB=30°,∠BDQ=∠CDP=60°
又∵△ABC等边三角形
∴∠ABC=∠ACB=60°
∴∠MBD=∠PCD=30°,CQ⊥AB,BP⊥AC,
∴AQ=BQ=![]() AB=
AB=![]() ,AP=PC=
,AP=PC=![]() AC=
AC=![]() ,
,
在△BDQ和△CDP中,
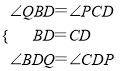 ,
,
∴△BDQ≌△CDP(ASA),
∴BQ=PC,QD=PD,
∵CQ⊥AB,BP⊥AC,
∴∠MQD=∠DPK=90°,
在△MDQ与△PDK中,
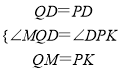 ,
,
∴△MDQ≌△PDK(SAS),
∴∠QDM=∠PDK,DM=DK,
∵∠BDQ=60°∠MDN=60°,
∴∠QDM+∠PDN=60°,
∴∠PDK+∠PDN=60°,
即∠KDN=60°,
在△MDN与△KDN中,
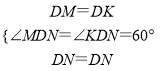 ,
,
∴△MDN≌△KDN(SAS),
∴MN=KN=NP+PK,
∴△AMN的周长=AM+AN+MN=AM+AN+NP+PK=AM+AN+NP+QM=AQ+AP=![]() +
+![]() =3
=3
故△AMN的周长为3.


科目:初中数学 来源: 题型:
【题目】某文具店去年8月底购进了一批文具1160件,预计在9月份进行试销.购进价格为每件10元.若售价为12元/件,则可全部售出.若每涨价0.1元.销售量就减少2件.
(1)求该文具店在9月份销售量不低于1100件,则售价应不高于多少元?
(2)由于销量好,10月份该文具进价比8月底的进价每件增加20%,该店主增加了进货量,并加强了宣传力度,结果10月份的销售量比9月份在(1)的条件下的最低销售量增加了m%,但售价比9月份在(1)的条件下的最高售价减少![]() m%.结果10月份利润达到3388元,求m的值(m>10).
m%.结果10月份利润达到3388元,求m的值(m>10).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30,点M、N分别是射线OB、OA上的动点,点P为∠AOB内一点,且OP=8,则△PMN的周长的最小值=___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与坐标轴分别交于A、B两点,已知点A的坐标为(0,8),点B的坐标为(8,0),OC、AD均是△OAB的中线,OC、AD相交于点F,OE⊥AD于G交AB于E.
(1)点C的坐标为__________;
(2)求证:△AFO≌△OEB;
(3)求证:∠ADO=∠EDB

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com