
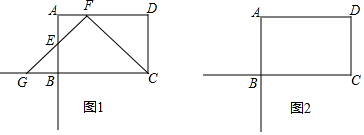
���� ��1����ͼ1�У���FH��CG��H��ֻҪ֤����FGH�ǵ���ֱ�������μ��ɣ�
��2����ȫͼ�Σ���ͼ2��ʾ����Rt��FDC�У����CF���ɽ�����⣻
��3���ⷨһ������F��FK��BC�ڵ�K����ͼ3��ֻҪ֤����FGK�ա�EGB���ɽ�����⣻�ⷨ����ֻҪ֤��BG=BH=x���Ƴ�CG=HG=2x���ɵ�x+2x=12���ⷽ�̼��ɣ�
��� �⣺��1����ͼ1�У���FH��CG��H��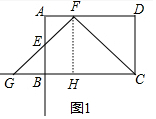
��Rt��FGH��FG=8$\sqrt{2}$��FH=CD=8��
��GH=$\sqrt{F{G}^{2}-F{H}^{2}}$=8��
��FH=GH��
���GFH=45�㣬
�ߡ�AFH=90�㣬
���AFG=��DFC=45�㣬
���GFC=180��-45��-45��=90�㣮
�ʴ�Ϊ90�㣮
��2����ȫͼ�Σ���ͼ2��ʾ�� 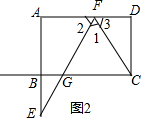
���ı���ABCD�Ǿ��Σ�
��BC=AD=12����D=90�㣮
�ߡ�GFC�ǵȱ������Σ�
��GC=FC����1=60�㣬
�ߡ�2=��3��
���3=60�㣬
��Rt��CDF��DC=8��
��FC=$\frac{16\sqrt{3}}{3}$��
��GC=FC=$\frac{16\sqrt{3}}{3}$��
��BG=12-$\frac{16\sqrt{3}}{3}$��
��3���ⷨһ������F��FK��BC�ڵ�K����ͼ3��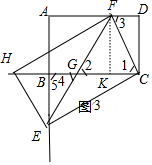
���ı���ABCD�Ǿ��Σ�
���5=��ABC=90�㣬AD��BC��
���1=��3����2=��AFG��
�ߡ�3=��AFG��
���1=��2��
��FG=FC��
��GK=CK��
���ı���FHEC��ƽ���ı��Σ�
��FG=EG��
�ߡ�2=��4����FKG=��5=90�㣬
���FGK�ա�EGB��
��BG=GK=KC=$\frac{12}{3}$=4��
�൱BG=4ʱ����F��H��E��CΪ������ı�����ƽ���ı��Σ�
�ⷨ������ͼ4��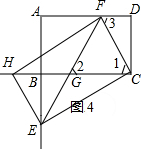
���ı���ABCD�Ǿ��Σ�
���ABG=90�㣬AD��BC��
���1=��3����2=��AFG��
�ߡ�3=��AFG��
���1=��2��
��FG=FC��
���ı���FHEC��ƽ���ı��Σ�
��CG=HG��FG=EG��HE=FC��
��EG=EH��
�֡ߡ�ABG=90�㣬
��BG=BH=x��
��CG=HG=2x��
��x+2x=12��
��x=4��
�൱BG=4ʱ����F��H��E��CΪ������ı�����ƽ���ı��Σ�
���� ���⿼���ı����ۺ��⡢���ε����ʡ�ƽ���ı��ε����ʡ����������ε��ж������ʡ�ȫ�������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����Ӹ����߽�����⣬�����п�ѹ���⣮


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Խ�������� | B�� | ���߶�AB=10cm | C�� | ��a=b����-a=-b | D�� | ����A��B���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Ϊ�������� | B�� | Ϊ���⸺���� | ||
| C�� | ����0��Ϊ���ⲻ����-1�ĸ����� | D�� | Ϊ������-1�ķ������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
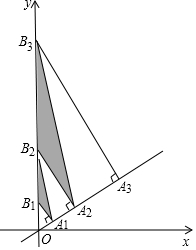 ��ͼ��ֱ��y=$\frac{{\sqrt{3}}}{3}$x���е�A1��A2��A3����An+1����OA1=1��A1A2=2��A2A3=4��AnAn+1=2n���ֱ����A1��A2��A3����An+1��ֱ��y=$\frac{{\sqrt{3}}}{3}$x�Ĵ��ߣ���y���ڵ�B1��B2��B3����Bn+1����������A1B2��A2B3��A3B4����AnBn+1���õ���A1B1B2����A2B2B3����A3B3B4��������AnBnBn+1�����AnBnBn+1�����Ϊ��22n-1-2n-1��$\sqrt{3}$�����ú�������n��ʽ�ӱ�ʾ��
��ͼ��ֱ��y=$\frac{{\sqrt{3}}}{3}$x���е�A1��A2��A3����An+1����OA1=1��A1A2=2��A2A3=4��AnAn+1=2n���ֱ����A1��A2��A3����An+1��ֱ��y=$\frac{{\sqrt{3}}}{3}$x�Ĵ��ߣ���y���ڵ�B1��B2��B3����Bn+1����������A1B2��A2B3��A3B4����AnBn+1���õ���A1B1B2����A2B2B3����A3B3B4��������AnBnBn+1�����AnBnBn+1�����Ϊ��22n-1-2n-1��$\sqrt{3}$�����ú�������n��ʽ�ӱ�ʾ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com