
分析 (1)设菜籽有x吨,则花生有(100-x)吨,根据至少得到52吨植物油,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,取其内的最大正整数即可;
(2)设y=a%,根据销售总额=菜籽油的销售额+花生油的销售额结合今年的销售总额比去年下降$\frac{11}{20}$a%,即可得出关于y的一元二次方程,解之即可得出结论.
解答 解:(1)设菜籽有x吨,则花生有(100-x)吨,
根据题意得:56%(100-x)+56%x÷1.4≥52,
解得:x≤25.
答:菜籽至多有25吨.
(2)设y=a%,
根据题意得:[20+30(1+y)](1-y)=(20+30)(1-$\frac{11}{20}$y),
整理得:4y2-y=0,
解得:y=0.25或y=0(舍去),
∴a%=0.25,a=25.
答:a的值为25.
点评 本题考查了一元二次方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,列出关于x的一元一次不等式;(2)找准等量关系,列出关于y的一元二次方程.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
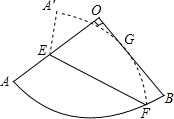 如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是$\widehat{AB}$上一点.将扇形AOB沿EF对折,使得折叠后的圆弧$\widehat{A'F}$恰好与半径OB相切于点G.若OE=4,则O到折痕EF的距离为2$\sqrt{3}$.
如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是$\widehat{AB}$上一点.将扇形AOB沿EF对折,使得折叠后的圆弧$\widehat{A'F}$恰好与半径OB相切于点G.若OE=4,则O到折痕EF的距离为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
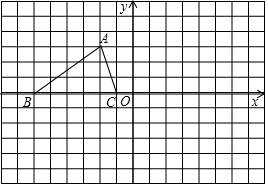 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0)
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com