
【题目】春节期间,小丽一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
租车公司:按日收取固定租金80元,另外再按租车时间计费.
共享汽车:无固定租金,直接以租车时间(时)计费.
如图是两种租车方式所需费用y1(元)、y2(元)与租车时间x(时)之间的函数图象,根据以上信息,回答下列问题:
(1)分别求出y1、y2与x的函数表达式;
(2)请你帮助小丽一家选择合算的租车方案.
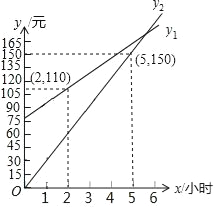
【答案】(1)y1=kx+80,y2=30x;(2)见解析.
【解析】
(1)设y1=kx+80,将(2,110)代入求解即可;设y2=mx,将(5,150)代入求解即可;
(2)分y1=y2,y1<y2,y1>y2三种情况分析即可.
解:(1)由题意,设y1=kx+80,
将(2,110)代入,得110=2k+80,解得k=15,
则y1与x的函数表达式为y1=15x+80;
设y2=mx,
将(5,150)代入,得150=5m,解得m=30,
则y2与x的函数表达式为y2=30x;
(2)由y1=y2得,15x+80=30x,解得x=![]() ;
;
由y1<y2得,15x+80<30x,解得x>![]() ;
;
由y1>y2得,15x+80>30x,解得x<![]() .
.
故当租车时间为![]() 小时时,两种选择一样;
小时时,两种选择一样;
当租车时间大于![]() 小时时,选择租车公司合算;
小时时,选择租车公司合算;
当租车时间小于![]() 小时时,选择共享汽车合算.
小时时,选择共享汽车合算.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】已知,AB、AC是圆O的两条弦,AB=AC,过圆心O作OH⊥AC于点H.
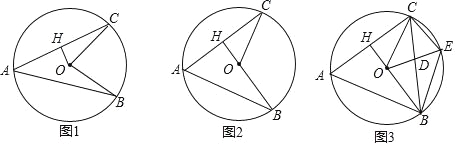
(1)如图1,求证:∠B=∠C;
(2)如图2,当H、O、B三点在一条直线上时,求∠BAC的度数;
(3)如图3,在(2)的条件下,点E为劣弧BC上一点,CE=6,CH=7,连接BC、OE交于点D,求BE的长和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
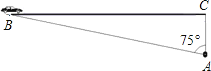
【题目】超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速.如图,观测点设在A处,离益阳大道的距离(AC)为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为8秒,∠BAC=75°.
(1)求B、C两点的距离;
(2)请判断此车是否超过了益阳大道60千米/小时的限制速度?
(计算时距离精确到1米,参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.732,![]() ,60千米/小时≈16.7米/秒)
,60千米/小时≈16.7米/秒)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(m-1)x2-(m-2)x+![]() m=0.
m=0.
(1)当m取何值时方程有一个实数根?
(2)当m取何值时方程有两个实数根?
(3)设方程的两根分别为x1、x2,且x1x2=m+1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
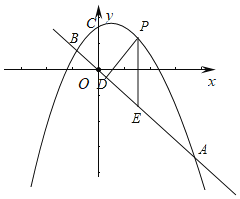
【题目】如图,已知抛物线y=-x2+bx+c与直线y=-x的交点A、B的横坐标分别为2和![]() .点P是直线上方抛物线上的一动点,过点P作PD⊥AB于点D,作PE⊥x轴交AB于点E.
.点P是直线上方抛物线上的一动点,过点P作PD⊥AB于点D,作PE⊥x轴交AB于点E.
(1)直接写出点A、B的坐标;
(2)求抛物线的关系式;
(3)判断△OBC形状,并说明理由;
(4)设点P的横坐标为n,线段PD的长为y,求y关于n的函数关系式;
(5)定义符号min{a,b)}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如min{2,0}=0,min{-3,4}=-3.直接写出min{-x2+bx+c,-x}的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图①,在矩形ABCD中,AB=2AD,E为CD的中点,则∠AEB ∠ACB(填“>”“<”“=”);
问题探究
(2)如图②,在正方形ABCD中,P为CD边上的一个动点,当点P位于何处时,∠APB最大?并说明理由;
问题解决
(3)如图③,在一幢大楼AD上装有一块矩形广告牌,其侧面上、下边沿相距6米(即AB=6米),下边沿到地面的距离BD=11.6米.如果小刚的睛睛距离地面的高度EF为1.6米,他从远处正对广告牌走近时,在P处看广告效果最好(视角最大),请你在图③中找到点P的位置,并计算此时小刚与大楼AD之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,
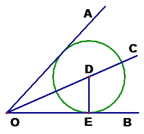
①判断⊙D与OA的位置关系, 并证明你的结论。
②通过上述证明,你还能得出哪些等量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沙坪坝区各街道居民积极响应“创文明城区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A,B两个社区,B社区居民人口数量不超过A社区居民人口数量的2倍.
(1)求A社区居民人口至少有多少万人?
(2)街道工作人员调查A,B两个社区居民对“社会主义核心价值观”知晓情况发现:A社区有1.2万人知晓,B社区有1.5万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A社区的知晓人数平均月增长率为m%,B社区的知晓人数第一个月增长了![]() m%,第二月在第一个月的基础上又增长了2m%,两个月后,街道居民的知晓率达到92%,求m的值.
m%,第二月在第一个月的基础上又增长了2m%,两个月后,街道居民的知晓率达到92%,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,过点
,过点![]() 做直线
做直线![]() 平行于
平行于![]() 轴,点
轴,点![]() 关于直线
关于直线![]() 对称点为
对称点为![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)点![]() 在直线
在直线![]() 上,且位于
上,且位于![]() 轴的上方,将
轴的上方,将![]() 沿直线
沿直线![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 恰好落在直线
恰好落在直线![]() 上,求点
上,求点![]() 的坐标和直线
的坐标和直线![]() 的解析式;
的解析式;
(3)设点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,当
上,当![]() 为等边三角形时,求点
为等边三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com