
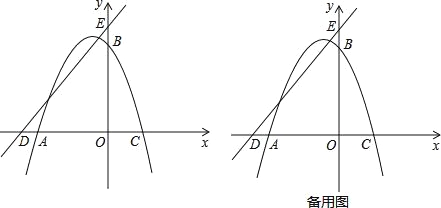
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬������y=ax2+2xa+c����A����4��0����B��0��4�����㣬��x�ύ����һ��C��ֱ��y=x+5��x�ύ�ڵ�D����y�ύ�ڵ�E��
��1���������ߵĽ���ʽ��
��2����P�ǵڶ������������ϵ�һ�����㣬����EP������E��EP�Ĵ���l����l�Ͻ�ȡ�߶�EF��ʹEF=EP���ҵ�F�ڵ�һ���ޣ�����F��FM��x���ڵ�M�����P�ĺ�����Ϊt���߶�FM�ij���Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£�����E��EH��ED��MF���ӳ����ڵ�H������DH����GΪDH���е㣬��ֱ��PG����AC���е�Qʱ�����F�����꣮
���𰸡���1��![]() ����2��d=5+t����3��F
����2��d=5+t����3��F![]() .
.
��������
�����������1��ֱ�Ӱ�A��B����������a��c��ֵ���ɣ���2���ֱ��P��F��y�������ߣ�����ֱ�ΪA����B������P��PN��x�ᣬ����ΪN����֤��PEA��ա�EFB�����ɵó�d=FM=OE��EB�����ٴ������ý���ʽ����3�������F��H�����꣬���ֵ�P�͵�H����������ȣ���PH��x��ƽ�У�����ƽ���߽��߶γɱ��������ɵ�GҲ��PQ���е㣬�ɴ˱�ʾ����G�����겢��ʽ�����t��ֵ��ȡ�ᣬ�������F�����꣮
�����������1���������![]() �����
����� ���������߽���ʽΪ
���������߽���ʽΪ![]() ����2���ֱ��P��F��y�������ߣ�����ֱ�ΪA����B������P��PN��x�ᣬ����ΪN����x=0ʱ��y=5����E��0��5������OE=5���ߡ�PEO+��OEF=90������PEO+��EPA��=90�������EPA��=��OEF����PE=EF����EA��P=��EB��F=90�������PEA��ա�EFB������PA��=EB��=��t����d=FM=OB��=OE��EB��=5������t��=5+t��
����2���ֱ��P��F��y�������ߣ�����ֱ�ΪA����B������P��PN��x�ᣬ����ΪN����x=0ʱ��y=5����E��0��5������OE=5���ߡ�PEO+��OEF=90������PEO+��EPA��=90�������EPA��=��OEF����PE=EF����EA��P=��EB��F=90�������PEA��ա�EFB������PA��=EB��=��t����d=FM=OB��=OE��EB��=5������t��=5+t��

��3����ͼ����ֱ��DE�Ľ���ʽΪ��y=x+5����EH��ED����ֱ��EH�Ľ���ʽΪ��y=��x+5��
��FB��=A��E=5������![]() t2��t+4��=
t2��t+4��=![]() t2+t+1����F��
t2+t+1����F��![]() t2+t+1��5+t��������H�ĺ�����Ϊ��
t2+t+1��5+t��������H�ĺ�����Ϊ��![]() t2+t+1��
t2+t+1��
y=��![]() t2��t��1+5=��
t2��t��1+5=��![]() t2��t+4����H��
t2��t+4����H��![]() t2+t+1����
t2+t+1����![]() t2��t+4������G��DH���е㣬��G��
t2��t+4������G��DH���е㣬��G�� ������G��
������G��![]() t2+
t2+![]() t��2����
t��2����![]() t2��
t2��![]() t+2������PH��x�ᣬ��DG=GH����PG=GQ��
t+2������PH��x�ᣬ��DG=GH����PG=GQ��
��![]() �����t=
�����t=![]() ����P�ڵڶ����ޣ���t��0����t=
����P�ڵڶ����ޣ���t��0����t=![]() ����F��
����F��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���÷�֤��֤�������ı�����������һ������ֱ�ǻ�۽ǡ�ʱ��Ӧ����________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
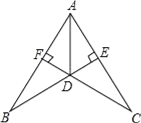
����Ŀ����ͼ��BE��AC��CF��AB�ڵ�E��F��BE��CF���ڵ�D��DE=DF������AD��
��֤����1����FAD=��EAD��
��2��BD=CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
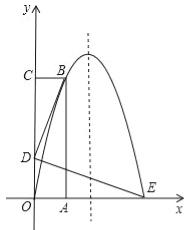
����Ŀ����ͼ��������OABC��OA����x����������ϣ�OC��y����������ϣ�������y=ax2+bx������B��1��4���͵�E��3��0�����㣮
��1���������ߵĽ���ʽ��
��2������D���߶�OC�ϣ���BD��DE��BD=DE����D������ꣻ
��3����������2���£��������ߵĶԳ�������һ��M��ʹ�á�BDM���ܳ�Ϊ��С�������BDM�ܳ�����Сֵ����ʱ��M�����ꣻ
��4����������2���£���B�㵽E����������ߵ�ͼ���ϣ��Ƿ����һ����P��ʹ�á�PAD�������������ڣ��������PAD��������ֵ����ʱP������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1����66��4+����2.5���£���0.1��
��2������2��3+����3����[����4��2+2]+����3��2�£���2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
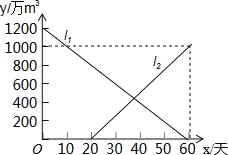
����Ŀ�����ڳ������º��������꣬ijˮ�����ˮ����ʱ������Ӷ����٣���֪ԭ����ˮ��y1����m3����ɺ�����ʱ��x���죩�Ĺ�ϵ��ͼ���߶�l1��ʾ��������ָɺ�������ӵ�20�쿪ʼ��ˮ��עˮ��עˮ��y2����m3����ʱ��x���죩�Ĺ�ϵ��ͼ���߶�l2��ʾ���������������أ���
��1����ԭ����ˮ��y1����m3����ʱ��x���죩�ĺ�����ϵʽ������x=20ʱ��ˮ������ˮ����
��2����0��x��60ʱ��ˮ�������ˮ��y����m3����ʱ��x���죩�ĺ�����ϵʽ��ע��x�ķ�Χ����������ˮ��������900��m3Ϊ���ظɺ���ֱ��д���������ظɺ�ʱx�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����28������������˨����ĸ����˨����ĸ������Ϊ1��2�պ����ף�ÿ��ÿ��ƽ��������˨12������ĸ18�����������������˨���裺��x������������˨��������������ĸ���������з���ӦΪ��������
A. 12x=18��28��x�� B. 2��12x=18��28��x��
C. 12��18x=18��28��x�� D. 12x=2��18��28��x��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017�������ڼ䣬����������7�������ÿ��Ӵ��ο͵�������ǰһ����ȵı仯�����������ʾ��ǰһ��������,������ʾ��ǰһ���ٵ����������±���
���� | 1�� | 2�� | 3�� | 4�� | 5�� | 6�� | 7�� |
�����仯/���� | +1.7 | +0.6 | +0.3 | -0.3 | -0.6 | +0.2 | -1.1 |
(1) ���ж��������ο���������������?���ٵ�������?��������������?
(2) ��9��30�յ��ο�����Ϊ3����,����7����ο��������Ƕ�������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒ���Ϊ200Ԫ������۵��������ۣ��Կɻ���20Ԫ���������Ʒ�Ľ���Ϊ�� ��
A.120Ԫ
B.100Ԫ
C.80Ԫ
D.60Ԫ
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com