
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.给出以下结论:①DG=DF;②四边形EFDG是菱形;③EG2=![]() GF×AF;④当AG=6,EG=2
GF×AF;④当AG=6,EG=2![]() 时,BE的长为
时,BE的长为![]() ,其中正确的编号组合是( )
,其中正确的编号组合是( )
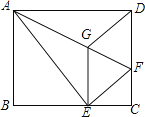
A.①②③B.①②④C.①③④D.①②③④
【答案】D
【解析】
先依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF,连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF=![]() GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系,过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD-GH求解即可.
GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系,过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD-GH求解即可.
解:∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.故①正确;
∴DG=GE=DF=EF.
∴四边形EFDG为菱形,故②正确;
如图1所示:连接DE,交AF于点O.
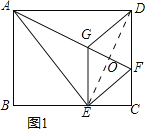
∵四边形EFDG为菱形,
∴GF⊥DE,OG=OF=![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴![]() =
=![]() ,即DF2=FOAF.
,即DF2=FOAF.
∵FO=![]() GF,DF=EG,
GF,DF=EG,
∴EG2=![]() GFAF.故③正确;
GFAF.故③正确;
如图2所示:过点G作GH⊥DC,垂足为H.
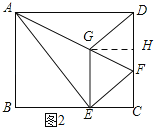
∵EG2=![]() GFAF,AG=6,EG=2
GFAF,AG=6,EG=2![]() ,
,
∴20=![]() FG(FG+6),整理得:FG2+6FG﹣40=0.
FG(FG+6),整理得:FG2+6FG﹣40=0.
解得:FG=4,FG=﹣10(舍去).
∵DF=GE=2![]() ,AF=10,
,AF=10,
∴AD=![]() =4
=4![]() .
.
∵GH⊥DC,AD⊥DC,
∴GH∥AD.
∴△FGH∽△FAD.
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴GH=![]() ,
,
∴BE=AD﹣GH=4![]() ﹣
﹣![]() =
=![]() .故④正确.
.故④正确.
故选:D.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于30%.试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每涨1元,每天销售量减少10本,现商店决定提价销售.设每天销售为![]() 本,销售单价为
本,销售单价为![]() 元.
元.
(1)请直接写出![]() 与
与![]() 之间的函数关系式和自变量
之间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)将足球纪念册销售单价定为多少元时,商店每天销售纪念册获得的利润![]() 元最大?最大利润是多少元?
元最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
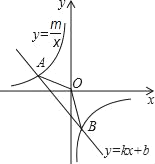
【题目】如图,已知A(4,2)、B(n,﹣4)是一次函数y=kx+b图象与反比例函数![]() 图象的两个交点.
图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)直接写出△AOB的面积;
(3)根据图象直接写出使一次函数的值小于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有甲、乙两座楼房,楼间距BC为50米,在乙楼顶部A点测得甲楼顶部D点的仰角为37°,在乙楼底部B点测得甲楼顶部D点的仰角为60°,则甲、乙两楼的高度分别为多少?(结果精确到1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】压岁钱由来已久,古称“厌胜钱”、“压祟钱”等.铛铛同学在2019年春节共收到10位长辈给的压岁钱,分别是:100元、200元、100元、50元、400元、300元、50元、100元、200元、400元.关于这组数据,下列说法正确的是( )
A.中位数是200元B.众数是100元
C.平均数是200元D.极差是300元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.如函数![]() ,当x=1时,y=3;当x=3时,y=1,即当
,当x=1时,y=3;当x=3时,y=1,即当![]() 时,有
时,有![]() ,所以说函数
,所以说函数![]() 是闭区间[1,3]上的“闭函数”.
是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2016]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2016]上的“闭函数”吗?请判断并说明理由;
(2)若二次函数y=![]() 是闭区间[1,2]上的“闭函数”,求k的值;
是闭区间[1,2]上的“闭函数”,求k的值;
(3)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的表达式(用含m,n的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com