
| 年份x | 1960 | 1974 | 1987 | 1999 | 2010 |
| 人口数量y(亿) | 30 | 40 | 50 | 60 | 69 |
分析 (1)根据增长的人口数除以年数,求得从1960年到2010年世界人口平均每年增长的数量;
(2)以1960年30亿人口为基础,根据世界人口平均每年增长的数量,求得人口数量y关于年份x的函数关系式;
(3)在所得的函数解析式中,求得当x=2020时函数的值即可.
解答 解:(1)从1960年到2010年世界人口平均每年增长(69-30)÷(2010-1960)=39÷50=0.78(亿);
(2)根据题意可得,
y=30+0.78(x-1960),
整理得函数的解析式为:y=0.78x-1498.8;
(3)当x=2020时,
y=0.78×2020-1498.8=76.8,
∴2020年世界人口将达到76.8亿人.
点评 本题主要考查了一次函数的应用,简单的一次函数问题主要有:①建立函数模型的方法;②分段函数思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,若△BCE的面积是6,则k的值为( )
如图,矩形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,若△BCE的面积是6,则k的值为( )| A. | -6 | B. | -8 | C. | -9 | D. | -12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{4}{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
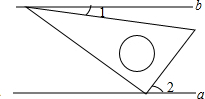 如图,将一块含有60°角的直角三角板的两个顶点放在两条平行的直线a,b上,如果∠2=50°,那么∠1的度数为( )
如图,将一块含有60°角的直角三角板的两个顶点放在两条平行的直线a,b上,如果∠2=50°,那么∠1的度数为( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com