
分析 (1)令x=b2+2ac,y=a2+c2根据三角形的三边关系即可得到结论;
(2)根据(2)的结论化简等式即可得到结论;
(3)过p作PD⊥AB于D,PE⊥AC于E,根据三角形的面积公式和题目中的公式即可得到结论.
解答 解:(1)令x=b2+2ac,y=a2+c2,
∴x-y=(b2+2ac)(a2+c2)=b2-(a2+c2-2ac)=b2-(a-c)2=(b+a-c)(b-a+c),
∵三角形两边之和大于第三边,
∴b+a-c>0,b-a+c>0,
∴x-y>0,
∴b2+2ac>a2+c2;
(2)∵b2+2ac>a2+c2,
∴(a2+c2)-(b2+2ac)<0,
∵$\frac{{x}^{2}-3x+2}{x}$+a2+c2-b2-2ac=0,
∴$\frac{{x}^{2}-3x+2}{x}$>0,
当1<x0<2时,x>0,x2-3x+2=(x-1)(x-2)<0,$\frac{{x}^{2}-3x+2}{x}$<0,
∴关于x的方程$\frac{{x}^{2}-3x+2}{x}$+a2+c2-b2-2ac=0不存在满足1<x0<2的实数根x0;
(3)过p作PD⊥AB于D,PE⊥AC于E,
∴S△ABC=$\frac{1}{2}$bcsin2θ=$\frac{1}{2}$c•PD=$\frac{1}{2}$b•PE,
∵∠BAC=2θ,AP是角平分线,
∴∠BAP=∠CAP=θ,
∴sinθ=$\frac{PD}{m}$,
∴PD=PE=sinθ•m,
∴S△ABC=$\frac{1}{2}$bcsin2θ=$\frac{1}{2}$c•sinθ•m+$\frac{1}{2}$b•sinθ•m=$\frac{1}{2}$sinθ•m(b+c),
∵sin2θ=2sinθcosθ,
∴m=$\frac{2bccosθ}{b+c}$.
点评 本题考查了三角形的三边关系,完全平方公式,三角函数,角平分线的性质,正确的运用公式是解题的关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
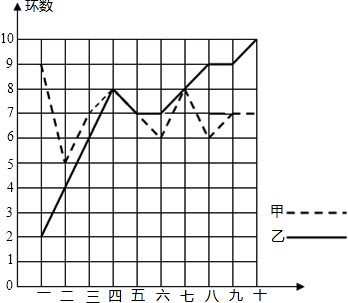 某市射击队甲、乙两名优秀队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
某市射击队甲、乙两名优秀队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:| 平均数 | 方差 | 中位数 | 命中9环(含9环) 以上的环数 | |
| 甲 | 7 | 7 | 1 | |
| 乙 | 5.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示).
某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com