
【题目】如图,在矩形ABCD中,将△ABD沿AB向下平移使A点到达B点,得到△BEC,下列说法正确的是( )
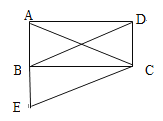
A. △ACE一定是等腰三角形B. △ACE一定是等边三角形
C. △ACE一定是锐角三角形D. △ACE不可能是等腰直角三角形
科目:初中数学 来源: 题型:
【题目】如图,已知三角形纸片![]() ,将纸片折叠,使点
,将纸片折叠,使点![]() 与点
与点![]() 重合,折痕分别与边
重合,折痕分别与边![]() 交于点
交于点![]() .
.
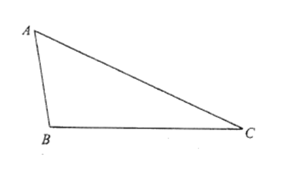
(1)画出直线![]() ;
;
(2)若点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,请画出点
,请画出点![]() ;
;
(3)在(2)的条件下,联结![]() ,如果
,如果![]() 的面积为2,
的面积为2,![]() 的面积为
的面积为![]() ,那么
,那么![]() 的面积等于 .
的面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3m,背水坡AD的坡度i(即tan∠DAB)为1:0.5,坝底AB=14m.
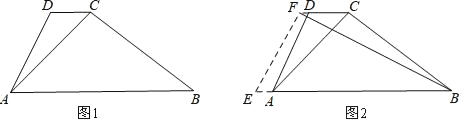
(1)求坝高;
(2)如图2,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底间时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明调查了班级里20位同学本学期购买课外书的花费情况,并将结果绘制成了如图的统计图.在这20位同学中,本学期购买课外书的花费的众数和中位数分别是( )

A. 50,50 B. 50,30 C. 80,50 D. 30,50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
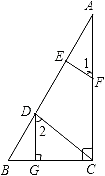
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定义)
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1=∠ (等量代换)
∴EF∥CD( )
∴∠AEF=∠ ( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°( )
∴CD⊥AB( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=α°,∠COD在∠AOB内部且∠COD=β°.
(1)若α,β满足|α-2β|+(β-60)2=0,则①α= ;
②试通过计算说明∠AOD与∠COB有何特殊关系;
(2)在(1)的条件下,如果作OE平分∠BOC,请求出∠AOC与∠DOE的数量关系;
(3)若α°,β°互补,作∠AOC,∠DOB的平分线OM,ON,试判断OM与ON的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
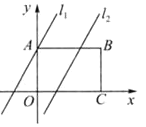
【题目】如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A,C在坐标轴上,点P在BC边上,直线ι1:y=2x+3,直线ι2:y=2x-3
(1)求直线l1与x轴的交点坐标T,直线ι2与AB的交点坐标Q和与x轴的交点坐标G;
(2)判定四边形ATGQ的形状并求它的面积;
(3)已知点M在第一象限,且是直线l2上的点,若ΔAPM是等腰直角三角形,求点M坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 在数轴上的位置如图所示,所对应的点分别为
在数轴上的位置如图所示,所对应的点分别为![]() .
.
![]()
(1)在数轴上表示![]() 的点与表示
的点与表示![]() 的点之间的距离为 ;由此可得点
的点之间的距离为 ;由此可得点![]() 之间的距离为
之间的距离为
(2)化简:![]()
(3)若![]() 的倒数是它本身,
的倒数是它本身,![]() 的绝对值的相反数是
的绝对值的相反数是![]() ,
,![]() 是数轴上表示
是数轴上表示![]() 的一点,且
的一点,且![]() ,求
,求![]() 所表示的数.
所表示的数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com