
����Ŀ����֪������ABCD�У�EΪ�Խ���BD��һ�㣬��E����EF��BD��BC��F������DF��GΪDF�е㣬����EG��CG��
��1����֤��EG=CG��
��2����ͼ���С�BEF��B����ʱ����ת45�㣬��ͼ����ʾ��ȡDF�е�G������EG��CG���ʣ�1���еĽ����Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
��3����ͼ���С�BEF��B����ת����Ƕȣ���ͼ����ʾ����������Ӧ���߶Σ��ʣ�1���еĽ����Ƿ���Ȼ������ͨ���۲��㻹�ܵó�ʲô���ۣ�����Ҫ��֤������
���𰸡�
��1��
֤�������ı���ABCD�������Σ�
���DCF=90�㣬
��Rt��FCD��
��GΪDF���е㣬
��CG= ![]() FD��
FD��
ͬ������Rt��DEF�У�
EG= ![]() FD��
FD��
��CG=EG��
��2��
�⣺��1���н�����Ȼ��������EG=CG��
֤��һ������AG����G����MN��AD��M����EF���ӳ��߽���N�㣮
�ڡ�DAG���DCG�У�

��AD=CD����ADG=��CDG��DG=DG��
���DAG�ա�DCG��SAS����
��AG=CG��
�ڡ�DMG���FNG�У�
�ߡ�DGM=��FGN��FG=DG����MDG=��NFG��
���DMG�ա�FNG��ASA����
��MG=NG��
�ߡ�EAM=��AEN=��AMN=90�㣬
���ı���AENM�Ǿ��Σ�
�ھ���AENM�У�AM=EN��
�ڡ�AMG���ENG�У�
��AM=EN����AMG=��ENG��MG=NG��
���AMG�ա�ENG��SAS����
��AG=EG��
��EG=CG��
֤�������ӳ�CG��M��ʹMG=CG��
����MF��ME��EC��

�ڡ�DCG���FMG�У�
��FG=DG����MGF=��CGD��MG=CG��
���DCG�ա�FMG��
��MF=CD����FMG=��DCG��
��MF��CD��AB��
��EF��MF��
��Rt��MFE��Rt��CBE��
��MF=CB����MFE=��EBC��EF=BE��
���MFE�ա�CBE
���MEF=��CEB��
���MEC=��MEF+��FEC=��CEB+��CEF=90�㣬
���MECΪֱ�������Σ�
��MG=CG��
��EG= ![]() MC��
MC��
��EG=CG��
��3��
�⣺��1���еĽ�����Ȼ�������������£�
��F��CD��ƽ���߲��ӳ�CG����M�㣬����EM��EC����F��FN��ֱ��AB��N��
����GΪFD�е㣬��֤��CDG�ա�MFG���õ�CD=FM��
����ΪBE=EF����֤��EFM=��EBC�����EFM�ա�EBC����FEM=��BEC��EM=EC
�ߡ�FEC+��BEC=90�㣬���FEC+��FEM=90�㣬����MEC=90�㣬
���MEC�ǵ���ֱ�������Σ�
��GΪCM�е㣬
��EG=CG��EG��CG��

����������1������ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬��֤��CG=EG����2��������Ȼ����������AG����G����MN��AD��M����EF���ӳ��߽���N�㣻��֤����DAG�ա�DCG���ó�AG=CG����֤����DMG�ա�FNG���õ�MG=NG����֤����AMG�ա�ENG���ó�AG=EG�����֤��CG=EG����3��������Ȼ��������֪��EG��CG��
�����㾫����������Ҫ������ȫ�������ε����ʺ������ε����ʵ����֪ʶ�㣬��Ҫ����ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����ȣ��������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������β�����ȷ�����⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A.3a+b=3ab
B.3a��a=2
C.2a3+3a2=5a5
D.��a2b+2a2b=a2b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������仯�����Ѿ�����������ĸ߶ȹ�ע���йز�����ȫ����Χ�ڶ�12��35��������Ⱥ�����˼�����������飬���Ƴ���������ͳ��ͼ��

�����ͼ�е���Ϣ���ش��������⣺
��1����γ��������й������������ˣ�
��2���벹ȫ����ͳ��ͼ��
��3������ͳ��ͼ��18��23�겿�ֵ�Բ�ĽǵĶ�����������
��4���ݱ�����Ŀǰ�ҹ�12��35���������ԼΪ2000�����������12��23�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���й涨����һ�ι������160kg���Ͽ���ԭ�۴��۳��ۣ�����160kg������160kg������ֻ�ܰ�ԭ�۳��ۣ�С���ҵ���������ף�ԭ�ƻ���Ĵ��ף�ֻ�ܰ�ԭ�۸����Ҫ600Ԫ��������40kg�����ۼ۸ǡ����ҪҲ��600Ԫ��
��1����С����ԭ�ƻ������������x��ǧ�ˣ��ķ�Χ��
��2������ԭ�۹���4kg����ۼ۹���5kg�Ŀ���ͬ����ôԭ�ƻ�С���ҹ�����ٴ��ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B��F��C��E��ֱ��l����F��C֮�䲻��ֱ�Ӳ���������A��D��l��࣬���AB=DE��AC=DF��BF=EC.

��1����֤����ABC�ա�DEF��
��2��ָ��ͼ������ƽ�е��߶Σ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
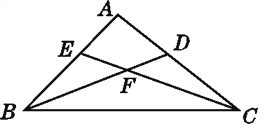
����Ŀ����ͼ,��CDΪ�����ߵ���������____________;��EFB��____________���ڽ�;����BCE��,BE���ԵĽ���____________,��CBE���Եı���____________;����AΪ�����ǵ���������____________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ3cm������P��B�������3cm/s���ٶ����ű�BC��CD��DA�˶�������A��ֹͣ�˶�����һ����Qͬʱ��B���������1cm/s���ٶ����ű�BA��A���˶�������A��ֹͣ�˶�����P���˶�ʱ��Ϊx��s������BPQ�����Ϊy��cm2������y����x�ĺ���ͼ���ǣ�������

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com