
| A. | y恒大于0 | B. | y恒小于0 | C. | y是非正数 | D. | 无法确定 |
分析 先由mn=7>0,m+n=-7<0,根据有理数的乘法与加法法则得出m<0,n<0.再计算y=-2(x-m)2+n的判别式△=(4m)2-4×(-2)(-2m2+n)=8n<0,得出二次函数y=-2(x-m)2+n与x轴没有交点,而a=-2<0,抛物线开口向下,根据二次函数的性质得到无论x取何值,y恒小于0.
解答 解:∵mn=7>0,
∴m与n符号相同,
∵m+n=-7<0,
∴m<0,n<0.
∵y=-2(x-m)2+n即为y=-2x2+4mx-2m2+n,
∴△=(4m)2-4×(-2)(-2m2+n)=8n<0,
∴二次函数y=-2(x-m)2+n与x轴没有交点,
又∵a=-2<0,抛物线开口向下,
∴无论x取何值,y恒小于0.
故选B.
点评 本题考查了二次函数的性质,有理数的乘法与加法法则等知识,计算出y=-2(x-m)2+n的判别式△=(4m)2-4×(-2)(-2m2+n)=8n<0是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 分数段(分) | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-100 |
| 人数 | 1 | 3 | 4 | 8 | 13 | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
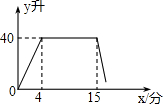 妈妈在用洗衣机洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示,根据图象解答下列问题:
妈妈在用洗衣机洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
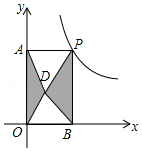 如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是3.
如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
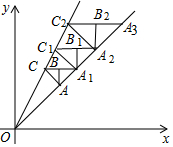 如图,在平面直角坐标系第一象限内,直线y=x与直线y=2x的内部作等腰Rt△ABC,是∠ABC=90°,边BC∥x轴,AB∥y轴,点A(1,1)在直线y=x上,点C在直线y=2x上:CB的延长线交直线y=x于点A1,作等腰Rt△A1B1C1,是∠A1B1C1=90°,B1C1∥x轴,A1B1∥y轴,点C1在直线y=2x上…按此规律,则等腰Rt△AnBnCn的腰长为$\frac{{4}^{n}}{{3}^{n+1}}$.
如图,在平面直角坐标系第一象限内,直线y=x与直线y=2x的内部作等腰Rt△ABC,是∠ABC=90°,边BC∥x轴,AB∥y轴,点A(1,1)在直线y=x上,点C在直线y=2x上:CB的延长线交直线y=x于点A1,作等腰Rt△A1B1C1,是∠A1B1C1=90°,B1C1∥x轴,A1B1∥y轴,点C1在直线y=2x上…按此规律,则等腰Rt△AnBnCn的腰长为$\frac{{4}^{n}}{{3}^{n+1}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com