
【题目】CD经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=∠![]() ,
,

(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠![]() =90°,则BE_____CF;EF____
=90°,则BE_____CF;EF____![]() .(填“>”“<”或“=”)
.(填“>”“<”或“=”)
②如图2,若0°<∠BCA<180°,请添加一个关于∠![]() 与∠BCA关系的条件__________,使①中的两个结论仍然成立,并证明两个结论成立.
与∠BCA关系的条件__________,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD经过∠BCA的外部,∠![]() =∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
【答案】(1)①=,=;②∠α+∠ACB=180°;(2)EF=BE+AF
【解析】
(1)①求出∠BEC=∠AFC=90°,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可;
②求出∠BEC=∠AFC,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可;
(2)求出∠BEC=∠AFC,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可.
解:(1)①如图1中,
E点在F点的左侧,
∵BE⊥CD,AF⊥CD,∠ACB=90°,
∴∠BEC=∠AFC=90°,
∴∠BCE+∠ACF=90°,∠CBE+∠BCE=90°,
∴∠CBE=∠ACF,
在△BCE和△CAF中,

∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,
∴EF=CF-CE=BE-AF,
当E在F的右侧时,同理可证EF=AF-BE,
∴EF=|BE-AF|
故答案为=,=;
②∠α+∠ACB=180°时,①中两个结论仍然成立;
证明:如图2中,
∵∠BEC=∠CFA=∠a,∠α+∠ACB=180°,
∴∠CBE=∠ACF,
在△BCE和△CAF中,

∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,
∴EF=CF-CE=BE-AF,
当E在F的右侧时,同理可证EF=AF-BE,
∴EF=|BE-AF|;
故答案为∠α+∠ACB=180°.
(2)结论:EF=BE+AF.
理由:如图3中,
∵∠BEC=∠CFA=∠a,∠a=∠BCA,
又∵∠EBC+∠BCE+∠BEC=180°,∠BCE+∠ACF+∠ACB=180°,
∴∠EBC+∠BCE=∠BCE+∠ACF,
∴∠EBC=∠ACF,
在△BEC和△CFA中,

∴△BEC≌△CFA(AAS),
∴AF=CE,BE=CF,
∵EF=CE+CF,
∴EF=BE+AF.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,某中学校园内有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划在中间留一块边长为(a+b)米的正方形地块修建一座雕像,然后将阴影部分进行绿化.

(1)求绿化的面积.(用含a、b的代数式表示)
(2)当a=2,b=4时,求绿化的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
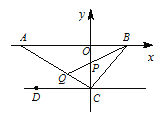
【题目】如图, A为x轴负半轴上一点, B为x轴正半轴上一点, C(0,-2),D(-3,-2).
(1)求△BCD的面积;
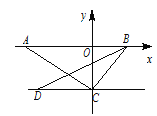
(2)若AC⊥BC,作∠CBA的平分线交CO于P,交CA于Q,判断∠CPQ与∠CQP的大小关系, 并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
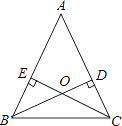
【题目】如图,△ABC的高BD,CE相交于点O.请你添加一个条件,使BD=CE.你所添加的条件是________.(仅添加一对相等的线段或一对相等的角)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线.
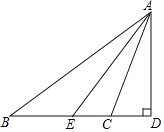
(1)求∠AEC的度数;
(2)过△ABC的顶点A作BC边上的高AD,求∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:
定义:如果一个数的平方等于-1,记为![]() =-1,这个数i叫做虚数单位,把形如a+bi (a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部.它的加,减,乘法运算与整式的加,减,乘法运算类似.例如,计算:
=-1,这个数i叫做虚数单位,把形如a+bi (a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部.它的加,减,乘法运算与整式的加,减,乘法运算类似.例如,计算:
(1-i )+(2+3i )=(1+2)+(-1+3)i=3+2i;
(1+i )×(3-i )=1×3-i+3×i-![]() =3+(-1+3)i+1=4+2i;
=3+(-1+3)i+1=4+2i;
根据以上信息,完成下列问题:
(1)填空:![]() =_______,
=_______,![]() =________;
=________;![]() =________;
=________;
(2)计算:(2+i )×(1-3i );
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.
(1)若∠A = 40°,求∠DCB的度数.
(2)若AE=4,△DCB的周长为13,求△ABC的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com