
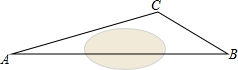
 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CAB=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CAB=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 分析 过点A作AD⊥BC,交BC延长线于点D,根据∠ABC=30°、∠CAB=15°求得∠CAD=45°,RT△ACD中由AC=200米知AD=ACcos∠CAD,再根据AB=$\frac{AD}{sin∠B}$可得答案.
解答 解:过点A作AD⊥BC,交BC延长线于点D,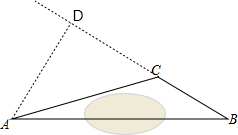
∵∠B=30°,
∴∠BAD=60°,
又∵∠BAC=15°,
∴∠CAD=45°,
在RT△ACD中,∵AC=200米,
∴AD=ACcos∠CAD=200×$\frac{\sqrt{2}}{2}$=100$\sqrt{2}$(米),
∴AB=$\frac{AD}{sin∠B}$=$\frac{100\sqrt{2}}{\frac{1}{2}}$=200$\sqrt{2}$≈283(米),
答:A,B两个凉亭之间的距离约为283米.
点评 本题主要考查解直角三角形的应用,根据已知条件构建合适的直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,已知?ABCD和?ABEF,连接AC、DF、CE、AE,AC与DF交于点G,若AC=DF=AE.
如图,已知?ABCD和?ABEF,连接AC、DF、CE、AE,AC与DF交于点G,若AC=DF=AE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形ABCD的两条对角线AC,BD相交于点O,若AC=4,BD=6,则菱形ABCD的周长为( )
如图,菱形ABCD的两条对角线AC,BD相交于点O,若AC=4,BD=6,则菱形ABCD的周长为( )| A. | 16 | B. | 24 | C. | 4$\sqrt{13}$ | D. | 8$\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
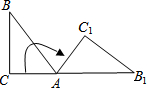 如图,在三角形ABC中,∠C=90°,∠B=35°,将三角形ABC绕点A按顺时针方向旋转到三角形AB1C1的位置,使得点C、A、B1在一条直线上,那么旋转角等于( )
如图,在三角形ABC中,∠C=90°,∠B=35°,将三角形ABC绕点A按顺时针方向旋转到三角形AB1C1的位置,使得点C、A、B1在一条直线上,那么旋转角等于( )| A. | 145° | B. | 125° | C. | 70° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com