
 某种产品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图.
某种产品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图.分析 (1)利用待定系数法求二次函数解析式得出即可;
(2)利用二次函数对称性得出每天的销售利润不低于16元时x的取值范围即可
解答 解:(1)由图象可得出:图象过(5,0),(7,16)点,
故$\left\{\begin{array}{l}{0=25a+5b-75}\\{16=49a+7b-75}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=20}\end{array}\right.$,
(2)∵函数y=-x2+20x-75图象的对称轴为直线x=10,
可知点(7,16)关于对称轴的对称点是(13,16),
又∵函数y=-x2+20x-75图象开口向下,
∴当7≤x≤13时,y≥16.
答:销售单价不少于7元且不超过13元时,该种商品每天的销售利润不低于16元.
点评 此题主要考查了二次函数的应用以及待定系数法求二次函数解析式等知识,正确利用二次函数对称性得出是解题关键.


科目:初中数学 来源: 题型:解答题
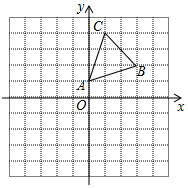 如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
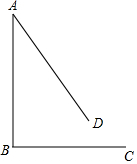 已知,AB=BC,∠ABC=90°.将线段AB绕点A逆时针旋转α(0°<α<90°)得到线段AD.点C关于直线BD的对称点为E,连接AE,CE.
已知,AB=BC,∠ABC=90°.将线段AB绕点A逆时针旋转α(0°<α<90°)得到线段AD.点C关于直线BD的对称点为E,连接AE,CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3cm,4cm,8cm | B. | 8cm,7cm,15cm | C. | 13cm,12cm,20cm | D. | 5cm,5cm,11cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC的顶点A,B,C的坐标分别是 A(-2,3).B(-3,2).C(-1,1).
如图,已知△ABC的顶点A,B,C的坐标分别是 A(-2,3).B(-3,2).C(-1,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.643×103立方米 | B. | 0.2643×108立方米 | ||
| C. | 26.43×106立方米 | D. | 2.643×107立方米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
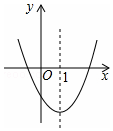 如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1,①b2>4ac;②4a-2b+c<0;③不等式ax2+bx+c>0的解集是x>3;④2a+b=0.其中判断正确的是①④.(只填写正确结论的序号)
如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1,①b2>4ac;②4a-2b+c<0;③不等式ax2+bx+c>0的解集是x>3;④2a+b=0.其中判断正确的是①④.(只填写正确结论的序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com