
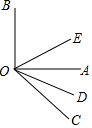
 如图所示,已知∠AOB=90°,∠AOC为锐角,OD平分∠AOC,OE平分∠BOC.
如图所示,已知∠AOB=90°,∠AOC为锐角,OD平分∠AOC,OE平分∠BOC.分析 根据角平分线定义得出∠COD=$\frac{1}{2}$∠AOC,∠EOC=$\frac{1}{2}$∠BOC,再根据∠DOE=∠EOC-∠COD=$\frac{1}{2}$∠AOB.
(1)将∠AOB=90°代入计算即可;
(2)将∠AOB=m°代入即可.
解答 解:∵OD平分∠AOC,OE平分∠BOC,
∴∠COD=$\frac{1}{2}$∠AOC,∠EOC=$\frac{1}{2}$∠BOC,
∴∠DOE=∠EOC-∠COD
=$\frac{1}{2}$∠BOC-$\frac{1}{2}$∠AOC
=$\frac{1}{2}$(∠BOC-∠AOC)
=$\frac{1}{2}$∠AOB.
(1)∵∠AOB=90°,
∴∠DOE=$\frac{1}{2}$×90°=45°;
(2)∵∠AOB=m°,
∴∠DOE=$\frac{1}{2}$m°.
点评 此题主要考查了角平分线的定义,根据图形得出所求角与已知角的关系是解题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:解答题
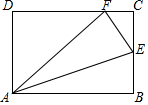 如图所示,将矩形ABCD沿AE折叠得到△AFE,且点D恰好落在DC上.
如图所示,将矩形ABCD沿AE折叠得到△AFE,且点D恰好落在DC上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
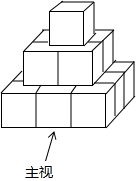 把棱长为1cm的若干个小正方体摆成如图所示的立体图形,然后在露出的表面上涂上颜色(不含底面).
把棱长为1cm的若干个小正方体摆成如图所示的立体图形,然后在露出的表面上涂上颜色(不含底面).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com