
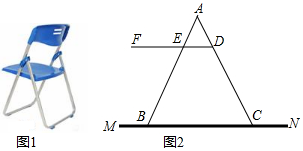
分析 (1)作DP⊥MN于点P,即∠DPC=90°,由DE∥MN知∠DCP=∠ADE=76°,根据DP=CDsin∠DCP可得答案;
(2)作EQ⊥MN于点Q可得四边形DEQP是矩形,知DE=PQ=20,EQ=DP=39,再分别求出BQ、CP的长可得答案.
解答 解:(1)如图,作DP⊥MN于点P,即∠DPC=90°,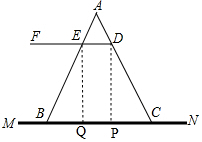
∵DE∥MN,
∴∠DCP=∠ADE=76°,
则在Rt△CDP中,DP=CDsin∠DCP=40×sin76°≈39(cm),
答:椅子的高度约为39厘米;
(2)作EQ⊥MN于点Q,
∴∠DPQ=∠EQP=90°,
∴DP∥EQ,
又∵DF∥MN,∠AED=58°,∠ADE=76°,
∴四边形DEQP是矩形,∠DCP=∠ADE=76°,∠EBQ=∠AED=58°,
∴DE=PQ=20,EQ=DP=39,
又∵CP=CDcos∠DCP=40×cos76°≈9.6(cm),
BQ=$\frac{EQ}{tan∠EBQ}$=$\frac{39}{tan58°}$≈24.4(cm),
∴BC=BQ+PQ+CP=24.4+20+9.6≈54(cm),
答:椅子两脚B、C之间的距离约为54cm.
点评 本题主要考查解直角三角形的应用,解直角三角形的一般过程是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
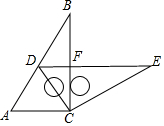 如图,两个含有30°角且大小相同的三角板(Rt△ABC和Rt△DCE)摆放在一起,直角顶点重合,点D刚好落在AB边上.
如图,两个含有30°角且大小相同的三角板(Rt△ABC和Rt△DCE)摆放在一起,直角顶点重合,点D刚好落在AB边上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
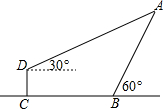 如图,一水库大坝AB的坡角为60°,在距离B点6米处有一平台CD,在D点测得点A的仰角为30°,已知点A,B,C,D在同一平面上,CD=2米,求这个大坝的高度.(结果保留很号)
如图,一水库大坝AB的坡角为60°,在距离B点6米处有一平台CD,在D点测得点A的仰角为30°,已知点A,B,C,D在同一平面上,CD=2米,求这个大坝的高度.(结果保留很号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com