
【题目】连接多边形任意两个不相邻顶点的线段称为多边形的对角线.
(1)
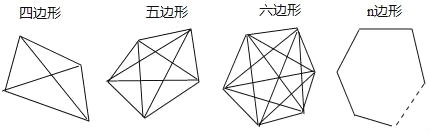
对角线条数分别为 、 、 、 .
(2)n边形可以有20条对角线吗?如果可以,求边数n的值;如果不可以,请说明理由.
(3)若一个n边形的内角和为1800°,求它对角线的条数.
【答案】(1)2;5;9;![]() ;(2)n边形可以有20条对角线,此时边数n为八;(3)这个多边形有54条对角线
;(2)n边形可以有20条对角线,此时边数n为八;(3)这个多边形有54条对角线
【解析】分析:(1)设n边形的对角线条数为an,根据多边形对角线条数公式即可求出结论;
(2)假设可以,根据多边形对角线条数公式,可得出关于n的一元二次方程,解之即可得出结论;
(3)根据多边形内角和定理,可求出边数,再套用多边形对角线条数公式,即可得出结论.
详解:(1)设n边形的对角线条数为an,
则a4=![]() =2,a5=
=2,a5=![]() =5,a6=
=5,a6=![]() =9,…,an=
=9,…,an=![]() .
.
(2)假设可以,根据题意得:
![]() =20,
=20,
解得:n=8或n=-5(舍去),
∴n边形可以有20条对角线,此时边数n为八.
(3)∵一个n边形的内角和为1800°,
∴180°×(n-2)=1800°,
解得:n=12,
∴![]() =
=![]() =54.
=54.
答:这个多边形有54条对角线.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=![]() (x>0)的图象经过菱形OACD的顶点D和边AC上的一点E,且CE=2AE,菱形的边长为8,则k的值为_____.
(x>0)的图象经过菱形OACD的顶点D和边AC上的一点E,且CE=2AE,菱形的边长为8,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在BD上,∠ABD=∠DBC,AB=BD,BE=BC,M,N分别是AE,CD的中点,连接MN,请判断△MBN的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列命题中:①过一点有且只有一条直线与已知直线平行;②平方根与立方根相等的数有![]() 和
和![]() ;③在同一平面内,如果
;③在同一平面内,如果![]() ,
,![]() ,则
,则![]() ;④直线
;④直线![]() 外一点
外一点![]() 与直线
与直线![]() 上各点连接而成的所有线段中,最短线段的长是
上各点连接而成的所有线段中,最短线段的长是![]() ,则点
,则点![]() 到直线
到直线![]() 的距离是
的距离是![]() ;⑤无理数包括正无理数、零和负无理数.其中真命题的个数是( )
;⑤无理数包括正无理数、零和负无理数.其中真命题的个数是( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
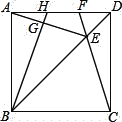
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足![]() 连接CE并延长交AD于点F,连接AE,过B点作
连接CE并延长交AD于点F,连接AE,过B点作![]() 于点G,延长BG交AD于点
于点G,延长BG交AD于点![]() 在下列结论中:
在下列结论中:
![]() ;
;![]() ;
;![]() ,其中正确的结论有
,其中正确的结论有![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
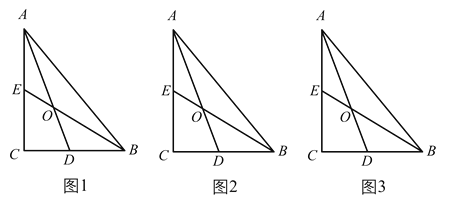
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点D,E分别在边BC,AC上.
,点D,E分别在边BC,AC上.
![]() 当
当![]() 时,直接写出
时,直接写出![]() ______,
______,![]() ______;
______;
![]() 如图2,若O为AD的中点,求证:
如图2,若O为AD的中点,求证:![]() ;
;
![]() 如图3,当
如图3,当![]() ,
,![]() 时,求AE的值.
时,求AE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
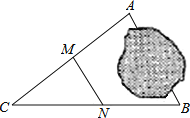
A. AB=24m B. MN∥AB
C. △CMN∽△CAB D. CM:MA=1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
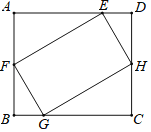
【题目】如图,矩形EFGH的四个顶点分别在矩形ABCD的各条边上,AB=EF,FG=2,GC=3.有以下四个结论:①∠BGF=∠CHG;②△BFG≌△DHE;③tan∠BFG=![]() ;④矩形EFGH的面积是4
;④矩形EFGH的面积是4![]() .其中一定成立的是______.(把所有正确结论的序号填在横线上)
.其中一定成立的是______.(把所有正确结论的序号填在横线上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com