
分析 (1)设组建中型两类图书室x个、小型两类图书室(30-x)个,由于组建中、小型两类图书室共30个,已知组建一个中型图书室需养殖类图书80本,种植类图书50本;组建一个小型图书室需养殖类图书30本,种植类图书60本,因此可以列出不等式组$\left\{\begin{array}{l}{80x+30(30-x)≤2000}\\{50x+60(30-x)≤1600}\end{array}\right.$,解不等式组然后去整数即可求解.
(2)根据(1)求出的数,分别计算出每种方案的费用即可.
解答 解:(1)设组建中型两类图书室x个、小型两类图书室(30-x)个.
由题意,得$\left\{\begin{array}{l}{80x+30(30-x)≤2000}\\{50x+60(30-x)≤1600}\end{array}\right.$,
化简得 $\left\{\begin{array}{l}{5x≤110}\\{x≥20}\end{array}\right.$,
解这个不等式组,得20≤x≤22.
由于x只能取整数,∴x的取值是20,21,22.
当x=20时,30-x=10;
当x=21时,30-x=9;
当x=22时,30-x=8.
故有三种组建方案:
方案一,中型图书室20个,小型图书室10个;
方案二,中型图书室21个,小型图书室9个;
方案三,中型图书室22个,小型图书室8个.
(2)方案一的费用是:2000×20+1500×10=55000(元);
方案二的费用是:2000×21+1500×9=55500(元);
方案三的费用是:2000×22+1500×8=56000(元);
故方案一费用最低,最低费用是55000元
点评 此题主要考查了一元一次不等式组在实际生活中的应用,解题的关键是首先正确理解题意,然后根据题目的数量关系列出不等式组解决问题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:解答题
 如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.
如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
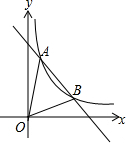 如图,已知反比例函数y=kx-1(k>0)的图象与一次函数图象y=-x+4交于a、b两点,点a的纵坐标为3.
如图,已知反比例函数y=kx-1(k>0)的图象与一次函数图象y=-x+4交于a、b两点,点a的纵坐标为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com