
如图,在□ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.
(1)判断四边形ABED的形状,并说明理由;
(2)判断直线DC与⊙O的位置关系,并说明理由;
(3)若AB=3,AE=6,求CE的长.
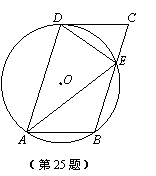 |

(1)四边形ABED是等腰梯形.
理由如下:在□ABCD中,AD∥BC,
∴∠DAE=∠AEB.
∴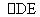 =
=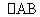 ,DE=AB.
,DE=AB.
∵AB∥CD,∴A B与DE不平行.
B与DE不平行.
∴四边形ABDE是等腰梯形.
 (2)直线DC与⊙O相切.
(2)直线DC与⊙O相切.
如图,作直径 DF,连接AF.
DF,连接AF.
于是,∠EAF=∠EDF.
∵∠DAE=∠CDE,
∴∠EAF+∠DAE=∠EDF+∠CDE,即∠DAF=∠CDF.
∵DF是⊙O的直径,点A在⊙O上,
∴∠DAF=90°,∴∠CDF=90°.∴OD⊥CD.
直线DC经过⊙O半径OD外端D,且与半径垂直,
直线DC与⊙O相切.
(3)由(1),∠EDA=∠DAB.
在□ABCD中,∠DAB=∠DCB,
∴∠EDA=∠DCB.又∵∠DAE=∠CDE,∴△ADE∽△DCE.∴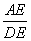 =
=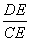 ,
,
∵AB=3,由(1)得,AB=DE=DC=3.即  =
= .
.
解得,CE= .
.


科目:初中数学 来源: 题型:
某物流公司的快递车和货车每天往返于甲、乙两地,快递车比货车多往返一趟.
已知货车比快递车早1小时出发,到达乙地后用1小时装卸货物,然后按原路以原速返回,
结果与第二趟返回的快递车同时到达甲地.下图表示快递车距离甲地的路程y(km)与货
车出发所用时间x(h)之间的函数关系图象.
(1)①请在下图中画出货车距离甲地的路程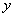 (km)与所用时间
(km)与所用时间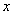 ( h)的函数关系图象;
( h)的函数关系图象;
②两车在中途相遇 次.
(2)试求货车从乙地返回甲地时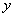 (km)与所用时间
(km)与所用时间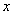 ( h)的函数关系式.
( h)的函数关系式.
(3)求快递车第二次从甲地出发到与返程货车相遇所用时间为多少h?这时货车离
乙地多少km?
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
震惊世界的M H370失联事件发生后第30天,中国“海巡01”轮在南印度洋海域搜索过程中首次侦听到疑是飞机黑匣子的脉冲信号,探测到的信号所在海域水深4500米左右,其中4500用科学记数法表示为_____
H370失联事件发生后第30天,中国“海巡01”轮在南印度洋海域搜索过程中首次侦听到疑是飞机黑匣子的脉冲信号,探测到的信号所在海域水深4500米左右,其中4500用科学记数法表示为_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com