
【题目】某校八年级学生在一次射击训练中,随机抽取10名学生的成绩如下表,请回答问题:
环数 | 6 | 7 | 8 | 9 |
人数 | 1 | 5 | 2 |
(1)填空:10名学生的射击成绩的众数是 ,中位数是 .
(2)求这10名学生的平均成绩.
(3)若9环(含9环)以上评为优秀射手,试估计全年级500名学生中有多少是优秀射手?
【答案】(1)7环,7环;(2)7.5环;(3)100名
【解析】
(1)根据众数、中位数的意义将10名学生的射击成绩排序后找出第5、6位两个数的平均数即为中位数,出现次数最多的数是众数.
(2)根据平均数的计算方法进行计算即可,
(3)样本估计总体,用样本中优秀人数的所占的百分比估计总体中优秀的百分比,用总人数乘以这个百分比即可.
解:(1)射击成绩出现次数最多的是7环,共出现5次,因此众数是7环,射击成绩从小到大排列后处在第5、6位的数都是7环,因此中位数是7环,
故答案为:7环,7环.
(2)10-1-5-2=2,![]() =7.5环,
=7.5环,
答:这10名学生的平均成绩为7.5环.
(3)500×![]() =100人,
=100人,
答:全年级500名学生中有100名是优秀射手.


科目:初中数学 来源: 题型:
【题目】高新一中初中校区名校+教育联合体主题美术展在西安高新区都市之门举办,学校组织七年级部分学生乘车参观展览,若用2辆小客车和1辆大客车,则每次可运送学生95人;若用1辆小客车和2辆大客车,则每次可运送学生115人(注意:每辆小客车和大客车都坐满).
(1)每辆小客车和大客车各能坐多少人?
(2)若现在要运送500名学生,计划租用小客车![]() 辆,大客车
辆,大客车![]() 辆,一次送完,且恰好每辆车都坐满,请你帮学校设计出所有的租车方案.
辆,一次送完,且恰好每辆车都坐满,请你帮学校设计出所有的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”的战略构想为国内许多企业的发展带来了新的机遇,某公司生产A,B两种机械设备,每台B种设备的成本是A种设备的1.5倍,公司若投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台.请解答下列问题:
(1)A、B两种设备每台的成本分别是多少万元?
(2)若A,B两种设备每台的售价分别是6万元,10万元,公司决定生产两种设备共60台,计划销售后获利不低于126万元,且A种设备至少生产53台,求该公司有几种生产方案;
(3)在(2)的条件下,销售前公司决定从这批设备中拿出一部分,赠送给“一带一路”沿线的甲国,剩余设备全部售出,公司仍获利44万元,赠送的设备采用水路运输和航空运输两种方式,共运输4次,水路运输每次运4台A种设备,航空运输每次运2台B种设备(运输过程中产生的费用由甲国承担).直接写出水路运输的次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
![]() =1﹣
=1﹣![]() ,
,![]() ;
;![]() ,……,
,……,
将以上二个等式两边分别相加得:
![]() ++
++![]() +
+![]() =1﹣
=1﹣![]() +
+![]() ﹣
﹣![]() +
+![]() ﹣
﹣![]() =
=![]()
用你发现的规律解答下列问题:
(1)直接写出下列各式的计算结果:
①![]() +
+![]() +
+![]() +…+
+…+![]() = ;
= ;
②![]() +
+![]() +
+![]() +…+
+…+![]() = ;
= ;
(2)仿照题中的计算形式,猜想并写出:![]() = ;
= ;
(3)解方程:![]() +
+![]() +
+![]() =
=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校学生对以下四个电视节目:![]() 最强大脑
最强大脑![]() 、
、![]() 中国诗词大会
中国诗词大会![]() 、
、![]() 朗读者
朗读者![]() 、
、![]() 出彩中国人
出彩中国人![]() 的喜爱情况,随机抽取了部分学生进行调查,要求每名学生选出并且只能选出一个自己最喜爱的节目,根据调查结果,绘制了如下两幅不完整的统计图.
的喜爱情况,随机抽取了部分学生进行调查,要求每名学生选出并且只能选出一个自己最喜爱的节目,根据调查结果,绘制了如下两幅不完整的统计图.

请你根据图中所提供的信息,完成下列问题:
![]() 本次调查的学生人数为______;
本次调查的学生人数为______;
![]() 在扇形统计图中,A部分所占圆心角的度数为______;
在扇形统计图中,A部分所占圆心角的度数为______;
![]() 请将条形统计图补充完整;
请将条形统计图补充完整;
![]() 若该校共有3000名学生,估计该校最喜爱
若该校共有3000名学生,估计该校最喜爱![]() 中国诗词大会
中国诗词大会![]() 的学生有多少名.
的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,原点为O,已知一次函数的图象过点A(0,5),点B(﹣1,4)和点P(m,n)
(1)求这个一次函数的解析式;
(2)当n=2时,求直线AB,直线OP与x轴围成的图形的面积;
(3)当△OAP的面积等于△OAB的面积的2倍时,求n的值
查看答案和解析>>
科目:初中数学 来源: 题型:
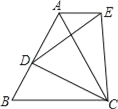
【题目】如图,等边△ABC中,D是AB边上的一动点,以CD为一边,向上作等边△EDC,连接AE.
(1)求证:△ACE≌△BCD;
(2)判断AE与BC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点A和点B(3,0),与
轴交于点A和点B(3,0),与![]() 轴交于点C(0,3).
轴交于点C(0,3).

(1)求抛物线的解析式;
(2)若点M是抛物线在![]() 轴下方上的动点,过点M作MN//
轴下方上的动点,过点M作MN//![]() 轴交直线BC于点N,求线段MN的最大值;
轴交直线BC于点N,求线段MN的最大值;
(3)在(2)的条件下,当MN取最大值时,在抛物线的对称轴![]() 上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC、△ADE中,C、E两点分别在AD、AB上,且BC与DE相交于F点,若∠A=90°,∠B=∠D=30°,AC=AE=1,则四边形AEFC的周长为何( )

A. 2![]() B. 2
B. 2![]() C. 2+
C. 2+![]() D. 2+
D. 2+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com