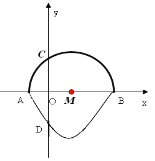
【题目】我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线。如图，点A、B、C、D分别是“蛋圆”与坐标轴的交点，点D的坐标为（0，-3）AB为半圆直径，半圆圆心M（1，0），半径为2，则经过点D的“蛋圆”的切线的解析式为__________________。
【答案】y=-2x-3
【解析】
试题解:求切线解析式需要先求出二次函数解析式，因为切线过点D，所以切线解析式与二次函数解析式组成方程组，因只有一个交点，所以判别式为零。∵M(1,0)半径=2，∴A(-1,0),B(3,0)，又D(0,-3),设二次函数的解析式为y=a(x-x1)(x-x2)，将点A,B,C代入得；-3a=-3,∴a=1，∴y=(x+1)(x-3)=x2-2x-3.∵切线与蛋圆只有一个交点，且经过点D,设切线解析式为y=kx+b,∵过点D,∴b=-3,x2-2x-3=kx-3 ,即-（2+k）2=0,∵只有一个交点，∴判别式△=0，解得k=-2,∴y=-2x-3.
名校课堂系列答案科目：初中数学 来源： 题型：
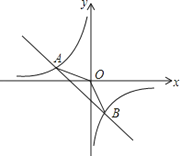
【题目】如图，在平面直角坐标系xOy中，一次函数y
=ax+b（a，b为常数，且a≠0）与反比例函数y
=
（m为常数，且m≠0）的图象交于点A（﹣2，1）、B（1，n）．
（1）求反比例函数和一次函数的解析式；
（2）连结OA、OB，求△AOB的面积；
（3）直接写出当y1＜y2＜0时，自变量x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
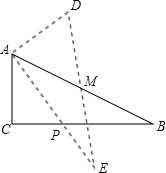
【题目】如图，在△ABC中，∠C=90°，AB=10，cosB=
，点M是AB边的中点，将△ABC绕着点M旋转，使点C与点A重合，点A与点D重合，点B与点E重合，得到△DEA，且AE交CB于点P，那么线段CP的长是__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，直线y＝x+2与双曲线
相交于点A（m，3）．
（1）求反比例函数的表达式；
（2）画出直线和双曲线的示意图；
（3）若P是坐标轴上一点，当OA＝PA时．直接写出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若一次函数y＝kx+b与反比例函数y＝
的图象如图所示，则关于x的不等式kx+b﹣≤﹣2的解集为（ ）
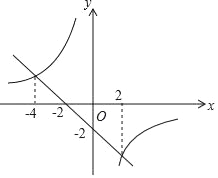
A. 0＜x≤2或x≤﹣4 B. ﹣4≤x＜0或x≥2
C. 
≤x＜0或x
D. x
或
查看答案和解析>>
科目：初中数学 来源： 题型：
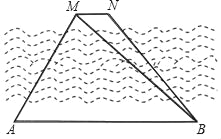
【题目】如图，在一条河的北岸有两个目标M、N，现在位于它的对岸设定两个观测点A、B．已知AB∥MN，在A点测得∠MAB＝60°，在B点测得∠MBA＝45°，AB＝600米．
(1)求点M到AB的距离；（结果保留根号）
(2)在B点又测得∠NBA＝53°，求MN的长．（结果精确到1米）
（参考数据：
≈1.732，sin53°≈0.8，cos53°≈0.6，tan53°≈1.33，cot53°≈0.75）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商品的进价为每件30元，售价为每件40元，每周可卖出180件；如果每件商品的售价每上涨1元，则每周就会少卖出5件，但每件售价不能高于50元，设每件商品的售价上涨x元（x为整数），每周的销售利润为y元．
（1）求y与x的函数关系式，并直接写出自变量x的取值范围；
（2）每件商品的售价为多少元时，每周可获得最大利润？最大利润是多少？
（3）每件商品的售价定为多少元时，每周的利润恰好是2145元？
查看答案和解析>>
科目：初中数学 来源： 题型：
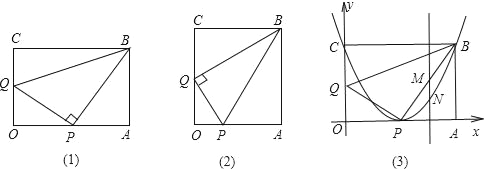
【题目】如图，已知矩形OABC，点P在边OA上（不与端点重合），点Q在边CO上（不与端点重合）．
（1）如图（1），若∠BPQ＝90°，且△OPQ与△PAB和△QPB相似，请写出表示这三个三角形相似的式子，并探究此时线段OQ、QB、BA之间的数量关系．
（2）若∠PQB＝90°，且△OPQ与△PAB、△QPB都相似，如图（2），请重新写出表示这三个三角形相似的式子，并证明AB：OA＝2
：3．
（3）在（1）中，若OA＝8
，OC＝8，OP＝CQ．以矩形OABC的两边OA、OC所在的直线分别为x轴和y轴，建立平面直角坐标系，如图（3），若某抛物线顶点为P，点B在抛物线上．
①求此抛物线的解析式．
②过线段BP上一动点M（点M与点P、B不重合），作y轴的平行线交抛物线于点N，若记点M的横坐标为m，试求线段MN的长L与m之间的函数关系式，画出该函数的示意图，并指出m取何值时，L有最大值，最大值是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
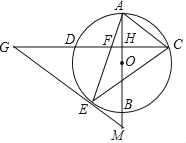
【题目】如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连结AC，过弧BD上一点E作EG∥AC交CD的延长线于点G，连结AE交CD于点F，且EG＝FG，连结CE．
（1）求证：△ECF∽△GCE；
（2）求证：EG是⊙O的切线；
（3）延长AB交GE的延长线于点M，若tan∠G＝
，AH＝3，求EM的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com