
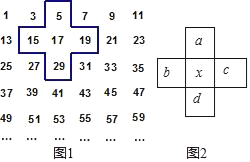
【题目】如图,将连续的奇数1,3,5,7…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.
(1)若x=17,则a+b+c+d= .
(2)移动十字框,用x表示a+b+c+d= .
(3)设M=a+b+c+d+x,判断M的值能否等于2020,请说明理由.
【答案】(1)68(2)4x(3)M的值不能等于2020
【解析】
(1)直接求和;
(2)a+b+c+d=(x﹣12)+(x﹣2)+(x+2)+(x+12),化简即可;
(3)令M=2020,则4x+x=2020,求出x,若x是奇数就说明成立,否则就不能为2020.
观察图1,可知:a=x﹣12,b=x﹣2,c=x+2,d=x+12.
(1)当x=17时,a=5,b=15,c=19,d=29,
∴a+b+c+d=5+15+19+29=68.
故答案为:68.
(2)∵a=x﹣12,b=x﹣2,c=x+2,d=x+12,
∴a+b+c+d=(x﹣12)+(x﹣2)+(x+2)+(x+12)=4x.
故答案为:4x.
(3)M的值不能等于2020,理由如下:
令M=2020,则4x+x=2020,
解得:x=404.
∵404是偶数不是奇数,
∴与题目x为奇数的要求矛盾,
∴M不能为2020.


科目:初中数学 来源: 题型:
【题目】计算:(1)![]() +(
+(![]() -
-![]() )÷(-
)÷(-![]() ); (2)-1-(1-
); (2)-1-(1-![]() )÷3×|3-9|;
)÷3×|3-9|;
(3)1![]() +(2.4×
+(2.4×![]() -
-![]() ×
×![]() )÷2
)÷2![]() ; (4)(-3-1
; (4)(-3-1![]() )÷[3
)÷[3![]() ÷(2-3
÷(2-3![]() )×1
)×1![]() ].
].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度,进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题: 
(1)参与调查的学生及家长共有人;
(2)在扇形统计图中,“基本了解”所对应的圆心角的度数是度;
(3)在条形统计图中,“非常了解”所对应的家长人数是人;
(4)若全校有1200名学生,请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
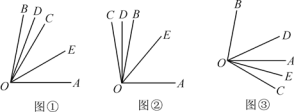
【题目】如图①,已知∠AOB=80°,OC是∠AOB内的一条射线,OD,OE分别平分∠BOC和∠COA.
(1)求∠DOE的度数;
(2)当射线OC绕点O旋转到OB的左侧时如图②(或旋转到OA的右侧时如图③),OD,OE仍是∠BOC和∠COA的平分线,此时∠DOE的大小是否和(1)中的答案相同?若相同,请选取一种情况写出你的求解过程;若不相同,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.问当P,Q同时出发,几秒时其中一个四边形为平行四边形?

查看答案和解析>>
科目:初中数学 来源: 题型:
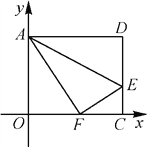
【题目】如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(10,8),求点E的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
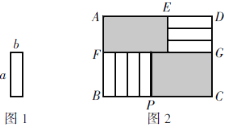
【题目】将7张如图1所示的长为a,宽为b(a>b)的小长方形纸片按图2所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,求a,b满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其顶点B的坐标为(3,﹣ ![]() ).
).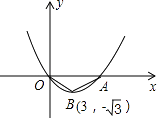
(1)求抛物线的函数解析式及点A的坐标;
(2)在抛物线上求点P,使S△POA=2S△AOB;
(3)在抛物线上是否存在点Q,使△AQO与△AOB相似?如果存在,请求出Q点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点 E、F分别为边 AD、CD上的动点(都与菱形的顶点不重合),联结 EF、BE、BF .
(1)若∠A=60°,且 AE+CF=AB,判断△BEF 的形状,并说明理由;
(2)在(1)的条件下,设菱形的边长为a,求△BEF面积的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com