
【题目】设二次函数![]() (
(![]() 为正常数)的图象与
为正常数)的图象与![]() 轴交于A、B两点(A在B的左侧),与
轴交于A、B两点(A在B的左侧),与![]() 轴交于C点.直线
轴交于C点.直线![]() 过M(0,m)(
过M(0,m)(![]() 且
且![]() )且与x轴平行,并与直线AC、BC分别相交于点D、E.二次函数
)且与x轴平行,并与直线AC、BC分别相交于点D、E.二次函数![]() 的图象关于直线
的图象关于直线![]() 的对称图象与y轴交于点P.设直线PD与
的对称图象与y轴交于点P.设直线PD与![]() 轴交点为Q ,则:
轴交点为Q ,则:
⑴ 求A、C两点的坐标;
⑵ 求![]() 的值(用含m的代数式表示);
的值(用含m的代数式表示);
⑶ 是否存在实数m,使![]() ?若能,则求出相应的m的值;若不能,请说明理由.
?若能,则求出相应的m的值;若不能,请说明理由.
【答案】⑴ 点C的坐标为(0,2).点A坐标为(-1,0).
⑵ AD=![]() .
.
⑶当![]() >1时,才存在实数m使得
>1时,才存在实数m使得![]() ∽
∽![]() ,从而有
,从而有![]() ,此时
,此时![]() ;当0<
;当0<![]() 1时,不存在实数m使得
1时,不存在实数m使得![]() .
.
【解析】试题分析:(1)令y=0,可得A点的坐标,令x=0,可得C点的坐标;(2)根据A、C两个点的坐标求出直线AC的解析式,再求出点D的坐标,然后求出对应线段的长度,最后利用勾股定理即可求出AD;(3)要使CD·AQ=PQ·DE,因为∠PQA=∠PDE=∠CDE,所以只须△PQA∽△CDE,即须△PQA∽△PDE,分0 <m<1,1<m<2两个情况讨论求解即可.
试题解析:
⑴ 令y=0,可得:0=-![]() (x+1)(x-a),
(x+1)(x-a),
解得x1=-1,x2=a,
∵A在B的左侧,a>0,
∴A(-1,0),
令x=0,可得:y=-![]() ×(-a)=2,
×(-a)=2,
∴C(0,2).
故点C的坐标为(0,2),点A坐标为(-1,0).
(2)
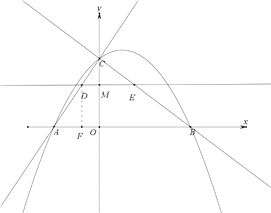
作DF⊥AB于点F,
∵A(-1,0),C(0,2),
∴直线AC解析式为:y=2x+2,
令y=m,m=2x+2,x=![]() -1,
-1,
∴D(![]() -1,m),
-1,m),
∴FO=1-![]() ,
,
∴AF=![]() ,
,
∵DF=m,
∴AD=![]() m.
m.
⑶连接AP、PE,
要使CD·AQ=PQ·DE,∵∠PQA=∠PDE=∠CDE,
∴只须△PQA∽△CDE,即须△PQA∽△PDE.

当0 <m<1时,点P在x轴下方,此时∠PQA显然为钝角,
而∠PDE显然为锐角,故此时不能有△PQA∽△CDE.
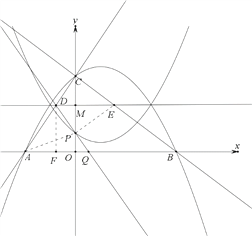
当1<m<2时,△PQA∽△PDE时,A、P、E三点共线,
∴△APO∽△EPM,
∴![]() =
=![]() ,
,
∵B(a,0),C(0,2),
∴直线BC解析式为:y=-![]() x+2,
x+2,
令![]() =
=![]() ,
,![]() =-
=-![]() +2,
+2,![]() =a-
=a-![]() ,
,
∴E(a-![]() ,m),
,m),
∴ME= a-![]() ,
,
∵CO=2,MO=m,
∴PM=CM=2-m,
∴PO=2m-2,
∴![]() =
=![]() ,
,
∴ ![]() ,而此时1<m<2,
,而此时1<m<2,
∴![]() ,
,
∴a>1.
综上所述,当a>1时,才存在实数m使得△PQA∽△CDE,从而有CD·AQ=PQ·DE,此时![]() ;当0<a≤1时,不存在实数
;当0<a≤1时,不存在实数![]() 使得CD·AQ=PQ·DE.
使得CD·AQ=PQ·DE.


科目:初中数学 来源: 题型:
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,以AD为边向外作Rt△ADE,∠AED=90°,连接OE.
⑴ 将△AOE绕点O顺时针旋转90°,得△A'OE'.
①画出△A'OE';②判断点E'是否在直线ED上,并说明理由;
⑵ 若DE=4,OE=![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办校级篮球赛,进入决赛的队伍有A、B、C、D,要从中选出两队打一场比赛.
(1)若已确定A打第一场,再从其余三队中随机选取一队,求恰好选中D队的概率.
(2)请用画树状图或列表法,求恰好选中B、C两队进行比赛的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)求证:BD1=CE1;(2)当∠CPD1=2∠CAD1时,求CE1的长;
(3)连接PA,△PAB面积的最大值为 .(直接填写结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为: ;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学课外活动小组在做气体压强实验时,获得压强p(Pa)与体积V(cm3)之间有下列对应数据:
p(Pa) | … | 1 | 2 | 3 | 4 | 5 | … |
V(cm3) | … | 6 | 3 | 2 | 1.5 | 1.2 | … |
根据表中提供的信息,回答下列问题:
(1)猜想p与V之间的关系,并求出函数关系式;
(2)当气体的体积是12cm3时,压强是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com