
【题目】在推进城乡生活垃圾分类的行动中,某校数学兴趣小组为了了解居民掌握垃圾分类知识的情况,对![]() 两小区各600名居民进行测试,从中各随机抽取50名居民成绩进行整理得到部分信息:
两小区各600名居民进行测试,从中各随机抽取50名居民成绩进行整理得到部分信息:
(信息一)![]() 小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
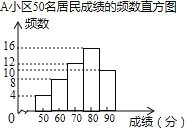
(信息二)上图中,从左往右第四组成绩如下:
75 | 77 | 77 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() 两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | ___________ | 79 | 40% | 277 |
| 75.1 | 77 | 76 | 45% | 211 |
根据以上信息,回答下列问题:
(1)求![]() 小区50名居民成绩的中位数;
小区50名居民成绩的中位数;
(2)请估计![]() 小区600名居民成绩能超过平均数的人数;
小区600名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,选择合适的统计量分析![]() 两小区参加测试的居民掌握垃圾分类知识的情况.
两小区参加测试的居民掌握垃圾分类知识的情况.
【答案】(1)76;(2)300人;(3)从平均数看,两个小区居民对垃圾分类知识掌握情况的平均水平相同;从方差看,B小区居民对垃圾分类知识掌握的情况比A小区稳定;从中位数看,B小区至少有一半的居民成绩高于平均数
【解析】
(1)因为有50名居民,中位数应为第25名和第26名成绩的平均值,所以中位数落在第四组,再根据信息二中的表格数据可得出结果;
(2)先求出A小区超过平均数的人数,即(16-1)+10=25(人),再根据![]() 小区600名居民成绩能超过平均数的人数=600×
小区600名居民成绩能超过平均数的人数=600×![]() ,即可得出结果;
,即可得出结果;
(3)从平均数看,两个小区居民对垃圾分类知识掌握情况的平均水平相同;从方差看,B小区居民对垃圾分类知识掌握的情况比A小区稳定;从中位数看,B小区至少有一半的居民成绩高于平均数.
解:(1)因为有50名居民,中位数应为第25名和第26名成绩的平均值.
而前三组的总人数为:4+8+12=24(人),所以中位数落在第四组,
第25名的成绩为75分,第26名的成绩为77分,所以中位数为76,
故答案为:76;
(2)根据题意得,600×![]() =300(人),
=300(人),
答:A小区600名居民成绩能超过平均数的人数300人;
(3)从平均数看,两个小区居民对垃圾分类知识掌握情况的平均水平相同;
从方差看,B小区居民对垃圾分类知识掌握的情况比A小区稳定;
从中位数看,B小区至少有一半的居民成绩高于平均数.
(答案不唯一,合理即可;)


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
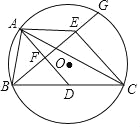
【题目】如图,△ABC内接于⊙O,AD是△ABC的中线,AE∥BC,射线BE交AD于点F,交⊙O于点G,点F是BE的中点,连接CE.
(1)求证:四边形ADCE为平行四边形;
(2)若BC=2AB,求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
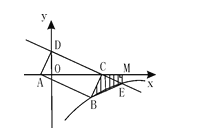
【题目】如图,直线y=-![]() x+2与x 轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=
x+2与x 轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=![]() (k<0)经过点B与直线CD交于E,EM⊥x轴于M,则SBEMC=______
(k<0)经过点B与直线CD交于E,EM⊥x轴于M,则SBEMC=______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
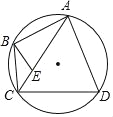
【题目】如图,四边形ABCD为圆内接四边形,A为弧BD中点,连接对角线AC,E在AC上,且AE=AB求证:
(1)∠CBE=![]() ∠CAD;
∠CAD;
(2)AC2=BCCD+AB2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰2个白色小正方形(每个白色小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是( )
的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰2个白色小正方形(每个白色小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=125°,则∠ADP的大小为( )
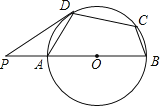
A.25°B.40°C.35°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.

(1)若∠FGB=∠FBG,求证:BF是⊙O的切线;
(2)若tan∠F=![]() ,CD=a,请用a表示⊙O的半径;
,CD=a,请用a表示⊙O的半径;
(3)求证:GF2﹣GB2=DFGF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同时抛掷两枚质地均匀的正四面体骰子,骰子各个面的点数分别是1至4的整数,把这两枚骰子向下的面的点数记为(a,b),其中第一枚骰子的点数记为a,第二枚骰子的点数记为b.
(1)用列举法或树状图法求(a,b)的结果有多少种?
(2)求方程x2+bx+a=0有实数解的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com