
 在直角梯形ABCD中,AB∥DC,.AB⊥BC,AB=2CD,E为AB的中点,若△EBC沿EC折叠,使B点落在AD上的F点,连结EF、CE、CF.
在直角梯形ABCD中,AB∥DC,.AB⊥BC,AB=2CD,E为AB的中点,若△EBC沿EC折叠,使B点落在AD上的F点,连结EF、CE、CF.分析 (1)根据题意和平行四边形的判定定理证明即可;
(2)根据三角形的面积公式得到$\frac{1}{2}$×BE×BC=16,根据完全平方公式求出BE+BC,根据三角形周长公式计算即可.
解答 解:(1)四边形AECD是平行四边形,
∵AB=2CD,E为AB的中点,
∴CD=AE,又AB∥DC,
∴四边形AECD是平行四边形;
(2)∵S四边形BCFE=32,
∴S△BEC=16,
∴$\frac{1}{2}$×BE×BC=16,
∵四边形AECD是平行四边形,
∴EC=AD=$4\sqrt{5}$,
∴BE2+BC2=EC2=80,
则(BE+BC)2=BE2+BC2+2×BE×BC=144,
∴BE+BC=12,
∴△ECB的周长=BE+BC+EC=12+4$\sqrt{5}$.
点评 本题考查的是翻折变换的性质和平行四边形的判定,找出翻折变换中的对应边和对应角是解题的关键.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 方程有无实数根,要根据k的取值而定 | |
| B. | 无论k取何值,方程必有两个不相等的实数根 | |
| C. | 当k>0时,方程有两正根;当k<0时,方程有两负根 | |
| D. | 因为-5<0,因此方程两根肯定都为负数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 汽车油箱中原有油50升,如果行驶中每小时用油5升,求油箱的油量y(单位:升)随行驶时间x(单位:时)变化的函数关系式,并写出自变量x的取值范围.
汽车油箱中原有油50升,如果行驶中每小时用油5升,求油箱的油量y(单位:升)随行驶时间x(单位:时)变化的函数关系式,并写出自变量x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
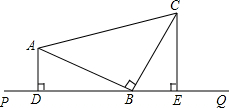 如图,△ABC中,AB=BC,∠ABC=90°,经过B点有一条直线PQ,分别过A、C作AD⊥PQ于D,CE⊥PQ于E.
如图,△ABC中,AB=BC,∠ABC=90°,经过B点有一条直线PQ,分别过A、C作AD⊥PQ于D,CE⊥PQ于E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com