
����Ŀ����1�����ں�������д���ʵ����ݣ���������֤����
��ͼ1��AB��CD����֤����B+��D=��BED��
֤��������E��һ��ֱ��EF��AB
���B=��BEF���� ��
��AB��CD��EF��AB
��EF��CD�� ��
���D=�� ��
���B+��D=��BEF+��FED
����B+��D=��BED��
��2����ͼ2��AB��CD����д����B+��BED+��D=360����������̣�
��3����ͼ3��AB��CD����ֱ��д�������B+��BEF+��EFD+��D= 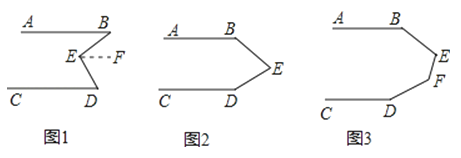
���𰸡���ֱ��ƽ�У��ڴ�����ȣ��������ֱ�߶��������ֱ��ƽ�У���ô������ֱ��Ҳ����ƽ�У���FED����ֱ��ƽ�У��ڴ�����ȣ���ͼ2������E��һ��ֱ��EF��AB����EF��AB�����B+��BEF=180�㣮��AB��CD��EF��AB����EF��CD�����FED+��D=180�㣬���B+��BEF+��FED+��D=180��+180��=360�㣬����B+��BED+��D=360�㣻540��
���������⣺��1������E��һ��ֱ��EF��AB��
��EF��AB��
���B=��BEF����ֱ��ƽ�У��ڴ�����ȣ���
��AB��CD��EF��AB��
��EF��CD���������ֱ�߶��������ֱ��ƽ�У���ô������ֱ��Ҳ����ƽ�У���
���D=��FED����ֱ��ƽ�У��ڴ�����ȣ���
��Ϊ����ֱ��ƽ�У��ڴ�����ȣ��������ֱ�߶��������ֱ��ƽ�У���ô������ֱ��Ҳ����ƽ�У���FED����ֱ��ƽ�У��ڴ�����ȣ�
��2����ͼ2������E��һ��ֱ��EF��AB��
��EF��AB��
���B+��BEF=180�㣮
��AB��CD��EF��AB��
��EF��CD��
���FED+��D=180�㣬
���B+��BEF+��FED+��D=180��+180��=360�㣬����B+��BED+��D=360��
��3����ͼ3���ֱ����EF��EG��AB��HF��CD��
��EG��AB��
���B+��BEG=180�㣮
��HF��CD��
���D+��HFD=180�㣮
��AB��CD��EG��AB��HF��CD��
��EG��HF��
���GEF+��HFE=180�㣬
���B+��BEF+��EFD+��D=540�㣮
���Դ��ǣ�540�㣮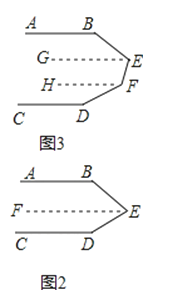
�����㾫��������ƽ���ߵ������ǽ����ĸ�������Ҫ֪����ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У��ڴ�����ȣ���ֱ��ƽ�У�ͬ���ڽǻ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶�CD���߶�AB�ϣ���CD=2�����߶�AB�ij�����һ������������ͼ����A��B��C��D���ĵ�����������Ϊ�˵�������߶γ���֮�Ϳ����ǣ� �� ![]()
A.28
B.29
C.30
D.31
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���y=��2��x��m��2��ͼ������˵������ȷ���ǣ� ��
A.��������
B.�Գ�����x=m
C.���ֵΪ0
D.��y��ཻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������̣�
��ͼ����֪DE��BC��DF��BE�ֱ�ƽ�֡�ADE����ABC�����Ƶá�FDE=��DEB�����ɣ�
��DE��BC����֪��
���ADE= ���� ��
��DF��BE�ֱ�ƽ�֡�ADE����ABC��
���ADF=![]()
��ABE=![]() ���� ��
���� ��
���ADF=��ABE
��DF�� ������
���FDE=��DEB���� ��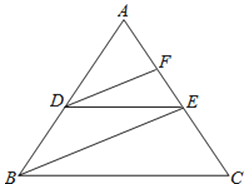
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�������������ֱ�ΪA��1��1����B��4��2����C��3��4����
��1���뻭����ABC����ƽ��5����λ���Ⱥ�õ�����A1B1C1��
��2���뻭����ABC����ԭ��ԳƵ���A2B2C2��
��3����x��������һ��P��ʹ��PAB���ܳ���С���뻭����PAB����ֱ��д��P�����꣮
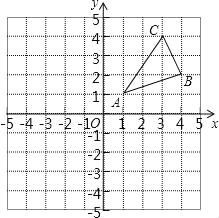
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ݽ������о�λ��ί�����ķ����������±���
ƽ���� | ��λ�� | ���� | ���� |
8.5 | 8.3 | 8.1 | 0.15 |
���ȥ��һ����߷ֺ�һ����ͷ֣����������һ���������仯���ǣ� ��
A.ƽ����
B.����
C.����
D.���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������;����������ô�����е�ʣ������y(L)����ʻ���x(km)֮��Ĺ�ϵʽy��50��0.1x����x��ȡֵ��Χ��_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��BD�ǡ�ABC�Ľ�ƽ���ߣ�DE��BC����AB�ڵ�E����A=45�㣬��BDC=72�㣬���BED�Ķ�����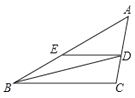
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪�߶�AB��CD�ཻ�ڵ�O������AC��BD�����ǰ�����ͼ1��ͼ�γ�֮Ϊ��8���Ρ�����ͼ2����CAB�͡�BDC��ƽ����AP��DP�ཻ�ڵ�P��������CD��AB�ֱ��ཻ��M��N���Խ���������⣺
��1����ϸ�۲죬��ͼ2���� �����߶�ACΪ�ߵġ�8���Ρ�
��2����ͼ2�У�����B=96�㣬��C=100�㣬���P�Ķ�����
��3����ͼ2�У������C=������B=�£���CAP=![]() ��CAB����CDP=
��CAB����CDP=![]() ��CDB�����ʡ�P���D����B֮�������������������ϵ���æ����±�ʾ��P������˵�����ɣ�
��CDB�����ʡ�P���D����B֮�������������������ϵ���æ����±�ʾ��P������˵�����ɣ�
��4����ͼ3�����A+��B+��C+��D+��E+��F�Ķ���Ϊ
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com