如图，四边形ABCD是平行四边形，点A（1，0），B（3，1），C（3，3）．反比例函数y=
（x＞0）的函数图象经过点D，点P是一次函数y=kx+3-3k（k≠0）的图象与该反比例函数图象的一个公共点．
（1）求反比例函数的解析式；
（2）通过计算，说明一次函数y=kx+3-3k（k≠0）的图象一定过点C；
（3）对于一次函数y=kx+3-3k（k≠0），当y随x的增大而增大时，确定点P的横坐标的取值范围（不必写出过程）．
阅读快车系列答案科目：初中数学 来源： 题型：解答题
平面直角坐标系
中，一次函数
和反比例函数
的图象都经过点
.
（1）求
的值和一次函数的表达式；
（2）点B在双曲线上，且位于直线的下方，若点B的横、纵坐标都是整数，直接写出点B的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
设
，
是任意两个不等实数，我们规定：满足不等式≤
≤
的实数的所有取值的全体叫做闭区间，表示为
. 对于一个函数，如果它的自变量与函数值
满足：当m≤≤n时，有m≤≤n，我们就称此函数是闭区间
上的“闭函数”.
（1）反比例函数
是闭区间
上的“闭函数”吗？请判断并说明理由；
（2）若一次函数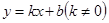
是闭区间上的“闭函数”，求此函数的表达式；
（3）若二次函数
是闭区间上的“闭函数”，直接写出实数， 的值.
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，一次函数y＝kx＋3的图象分别交x轴、y轴于点C、点D，与反比例函数
的图象在第四象限相交于点P，并且PA⊥x轴于点A，PB⊥y轴于点B，已知B（0，－6）且S△DBP＝27.
（1）求上述一次函数与反比例函数的表达式；
（2）设点Q是一次函数y＝kx＋3图象上的一点，且满足△DOQ的面积是△COD面积的2倍，直接写出点Q的坐标.
（3）若反比例函数
的图象与△ABP总有公共点，直接写出n的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，二次函数y=（x-2）2+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点．已知一次函数y=kx+b的图象经过该二次函数图象上点A（1，0）及点B．
（1）求二次函数与一次函数的解析式；
（2）根据图象，写出满足kx+b≥（x-2）2+m的x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，直线y＝－
x＋6分别与x轴、y轴交于A、B两点；直线y＝
x与AB交于点C，与过点A且平行于y轴的直线交于点D．点E从点A出发，以每秒1个单位的速度沿
轴向左运动．过点E作x轴的垂线，分别交直线AB、OD于P、Q两点，以PQ为边向右作正方形PQMN，设正方形PQMN与△ACD重叠部分（阴影部分）的面积为S（平方单位），点E的运动时间为t（秒）．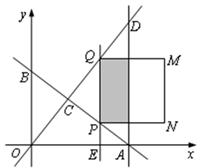
（1）求点C的坐标；
（2）当0＜t＜5时，求S与t之间的函数关系式，并求S的最大值；
（3）当t＞0时，直接写出点（4，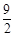
）在正方形PQMN内部时t的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
某地区冬季干旱，康平社区每天需从外地调运饮用水60吨．有关部门紧急部署，从甲、乙两水厂调运饮用水到供水点，甲厂每天最多可调出40吨，乙厂每天最多可调出45吨．从两水厂运水到康平社区供水点的路程和运费如下表：
| | 到康平社区供水点的路程（千米） | 运费（元/吨·千米） |
| 甲厂 | 20 | 4 |
| 乙厂 | 14 | 5 |
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
某公司准备与汽车租赁公司签订租车合同.以每月用车路程x(km)计算，甲汽车租赁公司的月租费
元，乙汽车租赁公司的月租费是
元.如果、与x之间的关系如图所示.
（1）求、与x之间的函数关系
（2）怎样选用汽车租赁比较合算？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
（2）见解析 （3）
＜a＜3
