
 如图,AC⊥BD于点C,F是AB上一点,FD交AC于点E,∠B与∠D互余.
如图,AC⊥BD于点C,F是AB上一点,FD交AC于点E,∠B与∠D互余.分析 (1)只要证明∠A+∠B=90°,∠D+∠B=90°即可解决问题;
(2)只要证明△ACB≌△DCF(ASA),即可推出BC=CE=1.5,由此即可解决问题;
解答 (1)证明:∵AC⊥BD,
∴∠A+∠B=90°,∠ACB=90°=∠DCE,
∵∠B+∠D=90°,
∴∠A=∠D.
(2)∵AE=1,AC=2.5,
∴EC=AC-AE=1.5,
∵∠B+∠D=90°,
∴∠BFD=90°,
∵∠ACB=90°,
∴∠BFD=∠ACD,
在△ACB和△DCF中,
$\left\{\begin{array}{l}{∠A=∠D}\\{AC=DC}\\{∠ACB=∠DCE}\end{array}\right.$,
∴△ACB≌△DCF(ASA),
∴BC=CE=1.5,
∴BD=BC+CD=4.
点评 本题考查全等三角形的判定和性质,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于点B的对称点.
如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于点B的对称点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∵∠1=∠2,∠2=∠3,∴∠1=∠3 | B. | ∵a∥b,b∥c,∴a∥c | ||
| C. | ∵∠1=∠2,∴$\frac{1}{2}$∠1=$\frac{1}{2}$∠2 | D. | ∵∠1+∠2=90°,∠1+∠3=90°,∴∠2=∠3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
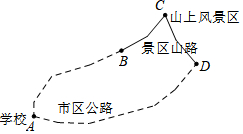 为了提倡“原色青春,绿色行走!”,某市某校组织学生从学校(点A)出发,沿A→B→C→D→A的路线参加总路程为14km绿色行走活动,其中路线A→B段、D→A段是我市区公路,B→C段、C→D段是景区山路.已知学生队伍在市区公路的行进速度为6km/h,在景区山路的行进速度为2km/h,本次行走共用3.5h.问本次行走活动中市区公路、景区山路各多少km?
为了提倡“原色青春,绿色行走!”,某市某校组织学生从学校(点A)出发,沿A→B→C→D→A的路线参加总路程为14km绿色行走活动,其中路线A→B段、D→A段是我市区公路,B→C段、C→D段是景区山路.已知学生队伍在市区公路的行进速度为6km/h,在景区山路的行进速度为2km/h,本次行走共用3.5h.问本次行走活动中市区公路、景区山路各多少km?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四边形的内角和为360° | |
| B. | 一条对角线平分另一条对角线的四边形是平行四边形 | |
| C. | 四边都相等的四边形是菱形 | |
| D. | 矩形的四个角都是直角 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com