
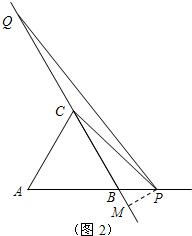
 解:(1)当0<x<a时,作PM⊥BQ(如图1),
解:(1)当0<x<a时,作PM⊥BQ(如图1),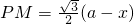 ,CQ=AP=x,所以S=
,CQ=AP=x,所以S=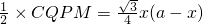 .
. 则
则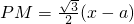 ,所以S=
,所以S=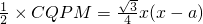 .
.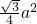 .
.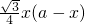 =
=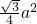 ,
,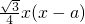 =
=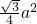 ,
,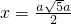 .
. 不合题意舍去,
不合题意舍去,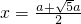 ,
,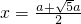 时,△PCQ的面积和△ABC的面积相等.
时,△PCQ的面积和△ABC的面积相等.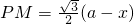 ,利用三角形的面积公式写出S与x的函数关系式即可;
,利用三角形的面积公式写出S与x的函数关系式即可;

 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
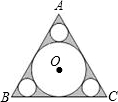 如图,已知正三角形ABC的边长为6,在△ABC中作内切圆O及三个角切圆(我们把与角两边及三角形内切圆都相切的圆叫角切圆),则△ABC的内切圆O的面积为
如图,已知正三角形ABC的边长为6,在△ABC中作内切圆O及三个角切圆(我们把与角两边及三角形内切圆都相切的圆叫角切圆),则△ABC的内切圆O的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
 点A运动.
点A运动.查看答案和解析>>
科目:初中数学 来源: 题型:
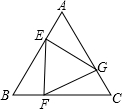 如图,已知正三角形ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是( )
如图,已知正三角形ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com