
【题目】如图,在射线AB上顺次取两点C,D,使AC=CD=1,以CD为边作矩形CDEF,DE=2,将射线AB绕点A沿逆时针方向旋转,旋转角记为α(其中0°<α<45°),旋转后记作射线AB′,射线AB′分别交矩形CDEF的边CF,DE于点G,H.若CG=x,EH=y,则下列函数图象中,能反映y与x之间关系的是( )
A.
B.
C.
D.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.关系:①AD∥BC;②AB=CD;③∠A=∠C;④∠B+∠C=180°.
(1)写出所有成立的情况(只需填写序号);
(2)选择其中一种证明.
已知:在四边形ABCD中, ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)四边形ABCD中,已知∠ABC+∠ADC=180°,AB=AD,DA⊥AB,点E在CD的延长线上,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)求证:CA平分∠BCD;
(3)如图(2),设AF是△ABC的BC边上的高,求证:EC=2AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
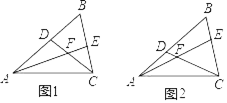
【题目】在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.
(1)如图1,若AE、CD为△ABC的角平分线:
①求∠AFD的度数;
②若AD=3,CE=2,求AC的长;
(2)如图2,若∠EAC=∠DCA=30°,求证:AD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为![]() ),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点
),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点![]()
![]()
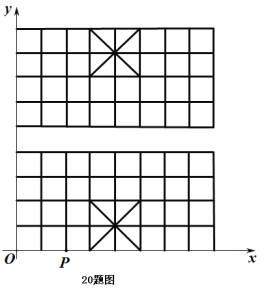
![]() 写出下一步“马”可能到达的点的坐标为_ (写出所有可能的点的坐标);
写出下一步“马”可能到达的点的坐标为_ (写出所有可能的点的坐标);
![]() 顺次连接
顺次连接![]() 中的所有点,得到的图形是 _图形(填“中心对称”或“轴对称”;
中的所有点,得到的图形是 _图形(填“中心对称”或“轴对称”;
![]() 将
将![]() 中得到的图形各顶点的坐标都乘以
中得到的图形各顶点的坐标都乘以![]() 请在平面直角坐标系中画出变化后的图形,并与原图形比较,形状和大小有怎样的变化?
请在平面直角坐标系中画出变化后的图形,并与原图形比较,形状和大小有怎样的变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是微信朋友圈热传的一篇文章.国际上,法国教育部宣布从2018年9月新学期起,小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图所示的统计图,已知“查资料”的人数是![]() 人.
人.

请你根据以上信息解答下列问题:
![]() 求出本次随机抽取的学生共有多少人;
求出本次随机抽取的学生共有多少人;
![]() 在扇形统计图中,“玩游戏”对应的百分比为______________,圆心角度数是_______________度;
在扇形统计图中,“玩游戏”对应的百分比为______________,圆心角度数是_______________度;
![]() 补全条形统计图;
补全条形统计图;
![]() 该校共有学生
该校共有学生![]() 人,估计每周使用手机时间在
人,估计每周使用手机时间在![]() 小时以上(不含
小时以上(不含![]() 小时)的人数.
小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知,![]() 满足
满足![]() 点在
点在![]() 轴的负半轴上,直角顶点
轴的负半轴上,直角顶点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上方.
轴上方.
![]() 如图1所示,若点
如图1所示,若点![]() 与原点重合,点
与原点重合,点![]() 的坐标是
的坐标是![]() ,则点
,则点![]() 的坐标是 ;
的坐标是 ;

![]() 如图2所示,若点
如图2所示,若点![]() 的坐标是
的坐标是![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,请求出点
,请求出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 | … |
下列四个结论:
①二次函数y=ax2+bx+c 有最小值,最小值为-3;
②抛物线与y轴交点为(0,-3);
③二次函数y=ax2+bx+c 的图像对称轴是x=1;
④本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com