
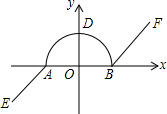 如图,在平面直角坐标系xOy中,我们把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段).已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.?当一次函数y=x+b的图象与图形C恰好只有一个公共点时,b的取值范围为b=$\sqrt{2}$或-1≤b<1;?已知?AMPQ(四个顶点A,M,P,Q按顺时针方向排列)的各顶点都在图形C上,且不都在两条射线上,则点M的横坐标x的取值范围为-2<x<-1或0≤x<$\frac{\sqrt{2}}{2}$.
如图,在平面直角坐标系xOy中,我们把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段).已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.?当一次函数y=x+b的图象与图形C恰好只有一个公共点时,b的取值范围为b=$\sqrt{2}$或-1≤b<1;?已知?AMPQ(四个顶点A,M,P,Q按顺时针方向排列)的各顶点都在图形C上,且不都在两条射线上,则点M的横坐标x的取值范围为-2<x<-1或0≤x<$\frac{\sqrt{2}}{2}$. 分析 利用直径所对的圆周角是直角,从而判定三角形ADB为等腰直角三角形,其直角边的长等于两直线间的距离,可利用数形结合的方法得到当直线与图形C有一个交点时自变量x的取值范围;
根据平行四边形的性质及其四个顶点均在图形C上,可能会出现四种情况,分类讨论即可得出答案.
解答  解:如图,分别连接AD、DB,则点D在直线AE上,
解:如图,分别连接AD、DB,则点D在直线AE上,
∵点D在以AB为直径的半圆上,
∴∠ADB=90°,
∴BD⊥AD,
在Rt△DOB中,由勾股定理得,BD=$\sqrt{2}$,
∵AE∥BF,
∴两条射线AE、BF所在直线的距离为$\sqrt{2}$,
则当一次函数y=x+b的图象与图形C恰好只有一个公共点时,b的取值范围是b=$\sqrt{2}$或-1≤b<1.
假设存在满足题意的平行四边形AMPQ,根据点M的位置,分以下四种情况讨论:
①当点M在射线AE上时,如图2,
∵AMPQ四点按顺时针方向排列,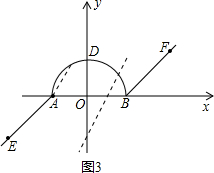
∴直线PQ必在直线AM的上方
∴PQ两点都在弧AD上,且不与点A、D重合,
∴0<PQ<$\sqrt{2}$.
∵AM∥PQ且AM=PQ,
∴0<AM<$\sqrt{2}$,
∴-2<x<-1,
②当点M在弧AD上时,如图3,
∵点A、M、P、Q四点按顺时针方向排列
∴直线PQ必在直线AM的下方,
此时,不存在满足题意的平行四边形.
③当点M在弧BD上时,
设弧DB的中点为R,则OR∥BF,
当点M在弧DB上时,如图4,
过点M作OR的垂线交弧DB于点Q,垂足为点S,可得S是MQ的中点.
∴四边形AMPQ为满足题意的平行四边形,
∴0≤x<$\frac{\sqrt{2}}{2}$.
当点M在弧RB上时,如图5,
直线PQ必在直线AM的下方,
此时不存在满足题意的平行四边形.
④当点M在射线BF上时,如图6,
直线PQ必在直线AM的下方,
此时,不存在满足题意的平行四边形.
综上,点M的横坐标x的取值范围是-2<x<-1或0≤x<$\frac{\sqrt{2}}{2}$.
故答案为:b=$\sqrt{2}$或-1<b<1,-2<x<-1或0≤x<$\frac{\sqrt{2}}{2}$.
点评 此题考查了一次函数的综合,题目中还涉及到了勾股定理、平行四边形的性质及圆周角定理的相关知识,题目中还渗透了分类讨论思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 已知抛物线y=ax2+bx+c(a≠0)经过点(-1,0),且顶点在第一象限.有下列三个结论:①a<0;②a+b+c>0;③-$\frac{b}{2a}$>0 ④abc>0.把正确结论的序号填在横线上①②③.
已知抛物线y=ax2+bx+c(a≠0)经过点(-1,0),且顶点在第一象限.有下列三个结论:①a<0;②a+b+c>0;③-$\frac{b}{2a}$>0 ④abc>0.把正确结论的序号填在横线上①②③.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
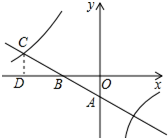 如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数$y=\frac{n}{x}$的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数$y=\frac{n}{x}$的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
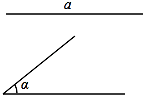 已知:线段a,∠α.
已知:线段a,∠α.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5>0.1 | B. | 0>$\frac{1}{5}$ | C. | -5.1<-4.2 | D. | 0<$-\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com