
 已知,正六边形ABCDEF在直角坐标系内的位置如图所示,点A的坐标为A(-1,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点B的经过的路径长是(2016$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
已知,正六边形ABCDEF在直角坐标系内的位置如图所示,点A的坐标为A(-1,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点B的经过的路径长是(2016$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$). 分析 根据正六边形的特点,每6次翻转为一个循环组循环,用2016除以6,根据商和余数的情况确定出点C的位置,然后求出翻转前进的距离,过点C作CG⊥x于G,求出∠CBG=60°,然后求出CG、BG,再求出OG,然后写出点C的坐标即可.
解答 解:∵正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,
∴每6次翻转为一个循环组循环,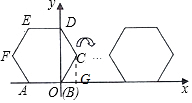
∵2016÷6=336,
∴经过2016次翻转为第336循环,点C在开始时的位置,
∵A(-1,0),
∴AB=1,
∴翻转前进的距离=1×2016=2016,
如图,过点C作CG⊥x于G,则∠CBG=60°,
∴OG=1×$\frac{1}{2}$=$\frac{1}{2}$,CG=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
∴OG=2016+$\frac{1}{2}$=2016$\frac{1}{2}$,
∴点B的坐标为(2016$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
故答案为(2016$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
点评 本题考查的是正多边形和圆,涉及到坐标与图形变化-旋转,正六边形的性质,确定出最后点C所在的位置是解题的关键,难点在于作辅助线构造出直角三角形.


科目:初中数学 来源: 题型:解答题
| 级数 | 全月应纳税所得额 | 税率% |
| 1 | 不超过500元的部分 | 5 |
| 2 | 超过500元至2000元的部分 | 10 |
| 3 | 超过2000元至5000元的部分 | 15 |
| 4 | 超过5000元至20000元的部分 | 20 |
| … | … |
| 公民 | 工资薪金(元) | 应纳税金(元) |
| 甲 | 2000 | 0 |
| 乙 | 2500 | 25 |
| 丙 | 3900 | 165 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
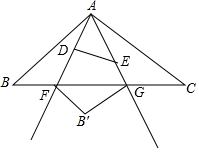 如图,在△ABC中,AB=AC=4,∠BAC=90°,以A为一个顶点的等腰Rt△ADE,∠ADE=90°,绕点A在∠BAC内旋转,AD、AE所在的直线与BC边分别交于点F、G,若点B关于直线AD的对称点为B′,当∠CFB′=60°时,则BF的长为$\frac{6\sqrt{2}-2\sqrt{3}}{3}$.
如图,在△ABC中,AB=AC=4,∠BAC=90°,以A为一个顶点的等腰Rt△ADE,∠ADE=90°,绕点A在∠BAC内旋转,AD、AE所在的直线与BC边分别交于点F、G,若点B关于直线AD的对称点为B′,当∠CFB′=60°时,则BF的长为$\frac{6\sqrt{2}-2\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{x+1}+\sqrt{x+2}+3=0$ | B. | $\sqrt{x-9}+\sqrt{4-x}=16$ | ||
| C. | $\sqrt{{x}^{2}+1}-\sqrt{{x}^{2}+2}=1-\frac{1}{\sqrt{{x}^{2}+1}}$ | D. | 6$\sqrt{{x}^{2}-2x+6}=21+2x-{x}^{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com