
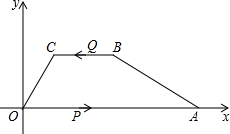
 四边形ABCO中,BC∥AO,BC与OA间的距离为$\sqrt{3}$,OA=6,∠AOC=60°,∠OAB=30°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).
四边形ABCO中,BC∥AO,BC与OA间的距离为$\sqrt{3}$,OA=6,∠AOC=60°,∠OAB=30°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).分析 (1)作CM⊥OA于点M,BR⊥OA于R,求出CM,BR的值,根据锐角三角形关系得出OM,AR的长,即可求出答案;
(2)作CM⊥OA于点M,BR⊥OA于R,根据三角形的面积求出得出函数关系式,再求最值即可;
(3)当Q在BC上,分为两种情况,根据勾股定理得出方程,求出即可;当Q在OC上,分为两种情况,求出每种情况,再进行判断,最后即可得出答案.
解答  解:(1)如图1,作CM⊥OA于点M,BR⊥OA于R,
解:(1)如图1,作CM⊥OA于点M,BR⊥OA于R,
∵∠AOC=60°,
∴∠OCM=30°,
∵BC与OA间的距离为$\sqrt{3}$,
∴CM=BR=$\sqrt{3}$,
∴MO=1,CO=2,AB=2$\sqrt{3}$,
∴AR=3,
∵AO=6,
∴BC=AO-MO-AR=2;
故答案为:2,2;
(2)如图2,作CM⊥OA于点M,
∵AR=3,BC=MR=2,
∵∠CMO=90°,∠OCM=30°,OM=1,
∴OC=2OM=2,
当动点Q运动到OC边时,OQ=4-t,
作QG⊥OP,∴∠OQG=30°,
∴OG=$\frac{1}{2}$OQ=$\frac{1}{2}$(4-t),
∴QG=$\frac{\sqrt{3}}{2}$(4-t),
又∵OP=2t,
∴S=$\frac{1}{2}$×2t×$\frac{\sqrt{3}}{2}$(4-t)=-$\frac{\sqrt{3}}{2}$(t2-4t)=-$\frac{\sqrt{3}}{2}$[(t-2)2-4]=-$\frac{\sqrt{3}}{2}$(t-2)2+2$\sqrt{3}$,
即△OPQ面积的最大值为:2$\sqrt{3}$;
(3)根据题意得出:0≤t≤3,
如图3,当0≤t≤2时,Q在BC边上运动,延长BC交y轴于点D,
此时OP=2t,OQ2=($\sqrt{3}$)2+(3-t)2,PQ2=($\sqrt{3}$)2+[2t-(3-t)]2,
∵∠POQ<∠POC=60°,
∴若△OPQ为直角三角形,只能是∠OPQ=90°或∠OQP=90°,
若∠OPQ=90°,如图3,则∠PQD=90°,
∴四边形PQDO为矩形,
∴OP=QD,
∴2t=3-t,
解得t=1,
若∠OQP=90°,如图4,
则OQ2+PQ2=PO2,
即(3-t)2+($\sqrt{3}$)2+(3t-3)2+($\sqrt{3}$)2=4t2,
解得:t1=t2=2,
当2<t≤3时,Q在OC边上运动,
若∠OQP=90°,
∵∠POQ=60°,
∴∠OPQ=30°,
∴$\frac{OQ}{OP}$=$\frac{1}{2}$,
若∠OPQ=90°,同理:$\frac{OP}{OQ}$=$\frac{1}{2}$,
而此时OP=2t>4,OQ<OC=2,
∴$\frac{OQ}{OP}$$≠\frac{1}{2}$,$\frac{OP}{OQ}$≠$\frac{1}{2}$,
故当Q在OC边上运动时,△OPQ不可能为直角三角形,
综上所述,当t=1或t=2时,△OPQ为直角三角形.
点评 本题考查了四边形综合以及含30°角的直角三角形、勾股定理、梯形的性质、坐标与图形的性质的应用等知识,利用分类讨论得出是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{6y=x+3}\\{7y=x+5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{6y=x-3}\\{7y+5=x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{6y=x+3}\\{7y+5=x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{6y=x-3}\\{7y=x+5}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≠2,b为任意实数 | B. | a=2,b≠0 | C. | a=2,b≠2 | D. | a,b为任意实数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com