
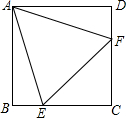
 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°③BE+DF=EF;④CE=$\sqrt{3}$,其中正确的结论的个数为( )
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°③BE+DF=EF;④CE=$\sqrt{3}$,其中正确的结论的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 只要证明Rt△ABE≌Rt△ADF(HL),可得BE=DF,连接AC交EF于G,可得EG=FG,根据正方形的性质、勾股定理等知识即可一一判断.
解答 解:∵四边形ABCD是正方形,
∴AB=AD, ∠B=∠D=90°,
∠B=∠D=90°,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{AE=AF}\end{array}\right.$,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC-BE=CD-DF,
∴CE=CF,故①正确;
∵CE=CF,
∴△ECF是等腰直角三角形,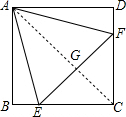
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,故②正确;
如图,连接AC,交EF于G点,
∴AC⊥EF,且AC平分EF,
∵∠FAD≠∠CAF,
∴DF≠FG,
∴BE+DF≠EF,故③错误;
∵EF=2,
∴CE=CF=$\sqrt{2}$,故④错误.
∴正确的有①②.
故选B.
点评 本题主要考查正方形的性质、全等三角形的判定和性质,线段的垂直平分线的判定和性质,角平分线的性质等知识,解答本题的关键是熟练掌握全等三角形的证明以及辅助线的正确作法,属于中考常考题型.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com