练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．已知m=$\frac{3n+25}{2n-5}$是正整数，那么n可以取4种不同的正整数．

    分析 将m化为1+$\frac{n+30}{2n-5}$，当n+30=2n-5时，n=35；当n+30＞2n-5时，n＜35；当n+30＜2n-5时，n＞35（不可能是正整数）；计算可得n的整整数值．

    解答 解：当n=3时，m=$\frac{3n+25}{2n-5}$=34；
    当n=5时，m=$\frac{3n+25}{2n-5}$=8；
    当n=9时，m=$\frac{3n+25}{2n-5}$=4；
    当n=35时，m=$\frac{3n+25}{2n-5}$=2；
    当n=3，5，9，35时，m=$\frac{3n+25}{2n-5}$时正整数；
    故答案为4．

    点评 本题考查了分式的值，确定m，n的值是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    7．已知a、b、c为△ABC的三边长，且a2+b2=8a+12b-52，其中c是△ABC中最短的边长，且c为整数，则c=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

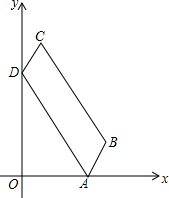    8．如图，在?ABCD中，∠BAD=60°，点A在x轴的正半轴上，点D在y轴的正半轴上，tan∠OAD=$\sqrt{3}$，AD和DC的长分别是方程x2-8x+12=0的两个根（AD＞DC）．
    （1）求点A的坐标；
    （2）求直线BC的解析式；
    （3）已知直线AB上有一点M，在坐标平面内是否存在一点N，使O，A，M，N为顶点的四边形是菱形？若存在，求出N点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．已知：当x1=a，x2=b，x3=c时，二次函数y=$\frac{1}{2}$x2+2mx对应的函数值分别为y1，y2，y3．若正整数a，b，c恰好是一个三角形的三边长，且当a＜b＜c时，都有y1＜y2＜y3，则实数m的取值范围是m＞-$\frac{5}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．半径为1的圆中，长度为1的弦所对的圆心角的度数是60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．一艘轮船从甲码头到乙码头顺流匀速行驶用了2小时，从乙码头返回甲码头逆流匀速行驶，用时不超过2.5小时，已知水流的速度为3km/h，若轮船在静水中的往返速度不变，轮船在静水中的速度应满足怎样的条件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．一副三角板，按如图所示摆放，已知AB=2，则CD=$\sqrt{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．分别写出下列各问题中的关系式，并指出各关系式中的常量和变量．
    （1）如果直角三角形中一个锐角的度数为α，另一个锐角的度数β与α之间的关系；
    （2）一支蜡烛原长为20cm，每分钟燃烧0.5cm，点燃x（分钟）后，蜡烛的长度y（cm）与x（分钟）之间的关系；
    （3）有一边长为2cm的正方形，若边长增加x cm，则增加的面积y（cm2）与x之间的关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．一个三角形的三条中位线的长分别为3，4，5，则三角形的面积为24．

    查看答案和解析>>

    同步练习册答案