

分析 (1)根据图形发现规律,利用规律写出第5个图形的棋子的个数即可;
(2)代入2014若能求得整数解即可,否则不可以.
解答 解:观察图形发现:第一个图形有6(1+1)-7=5个棋子,
第二个图形有6(2+1)-7=11个棋子,
第三个图形有6(3+1)-7=17个棋子,
…
第n个图形有6(n+1)-7=6n-1个棋子;
(1)第5个图形有6×(5+1)-7=29个棋子;
(2)当6n-1=2014时,
解得:n=$\frac{2015}{6}$,
∵n不是正整数,
∴不存在这样的图形由2014颗棋子组成.
点评 本题考查了图形的变化规律,解题的关键是仔细观察图形并发现其图形的变化规律,利用规律解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
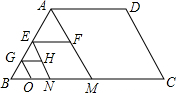 如图,四边形ABCD是等腰梯形,BC=2AD=4,过A作AM∥DC,得到第1个三角形,其平行于BC的中位线EF=1;过E作EN∥DC,得到第2个三角形,其平行于BC的中位线GH=$\frac{1}{2}$;过G作GO∥DC,得到第3个三角形,….按此规律作出第n个三角形,则其平行于BC的中位线长等于$\frac{1}{{2}^{n-1}}$.(用正整数n表示)
如图,四边形ABCD是等腰梯形,BC=2AD=4,过A作AM∥DC,得到第1个三角形,其平行于BC的中位线EF=1;过E作EN∥DC,得到第2个三角形,其平行于BC的中位线GH=$\frac{1}{2}$;过G作GO∥DC,得到第3个三角形,….按此规律作出第n个三角形,则其平行于BC的中位线长等于$\frac{1}{{2}^{n-1}}$.(用正整数n表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
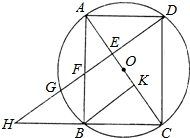 如图,已知:矩形ABCD,以对角线AC的中点O为圆心,OA的长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为点K,过点D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
如图,已知:矩形ABCD,以对角线AC的中点O为圆心,OA的长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为点K,过点D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=a,将矩形ABCD沿EF对折后,得ABFE和矩形EFCD,然后再把其中的一个矩形EFCD沿MN对折,得矩形MNCF和矩形MNDE,…,依此类推,得矩形PRSN和RQCS,并且所有矩形都相似,则RS等于( )
如图,在矩形ABCD中,AB=a,将矩形ABCD沿EF对折后,得ABFE和矩形EFCD,然后再把其中的一个矩形EFCD沿MN对折,得矩形MNCF和矩形MNDE,…,依此类推,得矩形PRSN和RQCS,并且所有矩形都相似,则RS等于( )| A. | $\frac{\sqrt{2}}{8}$a | B. | $\frac{\sqrt{2}}{4}$a | C. | $\frac{\sqrt{2}}{2}$a | D. | $\frac{1}{4}$a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
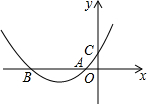 如图,抛物线y=ax2+bx+c与坐标轴的交点为A、B、C,且OA=OC=1,则下列关系中正确的是( )
如图,抛物线y=ax2+bx+c与坐标轴的交点为A、B、C,且OA=OC=1,则下列关系中正确的是( )| A. | a+b=-1 | B. | ac<0 | C. | b<2a | D. | a-b=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个正方形是相似图形 | |
| B. | 两个菱形是相似图形 | |
| C. | 底角相等的两个等腰三角形是相似图形 | |
| D. | 顶角相等的两个等腰三角形是相似图形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com