
| A. | $\sqrt{{x}^{2}+1}=0$ | B. | $\sqrt{x-2}+\frac{1}{2}=0$ | C. | $\sqrt{x+1}=2$ | D. | $\sqrt{x-1}+\sqrt{1-x}=2$ |
分析 先变形得出$\sqrt{a}$=k的形式,再根据二次根式的性质逐个进行判断即可.
解答 解:A、x2+1=0,
此时方程无解,故本选项错误;
B、∵$\sqrt{x-2}$+$\frac{1}{2}$=0,
∴$\sqrt{x-2}$=-$\frac{1}{2}$,
∵算术平方根是非负数,
∴此时方程无解,故本选项错误;
C、∵$\sqrt{x+1}$=2,
∴x+1=4,
∴x=3,
故本选项正确;
D、∵$\sqrt{x-1}$+$\sqrt{1-x}$=2,
∴x-1≥0且1-x≥0,
解得:x=1,
代入得:0+0=2,
此时不成立,故本选项错误;
故选C.
点评 本题考查了无理方程的应用,能根据二次根式的性质进行判断是解此题的关键.


科目:初中数学 来源: 题型:解答题
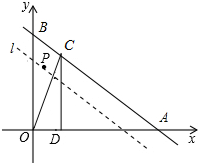 如图,已知点A(6$\sqrt{3}$,0),点B(0,6),经过AB的直线l以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
如图,已知点A(6$\sqrt{3}$,0),点B(0,6),经过AB的直线l以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果两直线平行,那么同位角相等 | |
| B. | 如果同位角相等,那么两直线平行 | |
| C. | 如果两个角相等,那么这两个角是同位角 | |
| D. | 如果两个角是同位角,那么这两个角相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 闵行体育公园内有一个形状是平行四边形的花坛(如图),并且AB∥EF∥DC,BC∥GH∥AD,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )
闵行体育公园内有一个形状是平行四边形的花坛(如图),并且AB∥EF∥DC,BC∥GH∥AD,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )| A. | 球落在红花丛中和绿花丛中的概率相等 | |
| B. | 球落在紫花丛中和橙花丛中的概率相等 | |
| C. | 球落在红花丛中和蓝花丛中的概率相等 | |
| D. | 球落在蓝花丛中和黄花丛中的概率相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com