
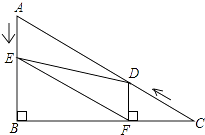
【题目】如图,在Rt△ABC中,∠B=90°,BC=5 ![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF. 
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
【答案】
(1)证明:在△DFC中,∠DFC=90°,∠C=30°,DC=2t,
∴DF=t.
又∵AE=t,
∴AE=DF
(2)解:能.理由如下:
∵AB⊥BC,DF⊥BC,
∴AE∥DF.
又AE=DF,
∴四边形AEFD为平行四边形.
∵AB=BCtan30°=5 ![]() =5,
=5,
∴AC=2AB=10.
∴AD=AC﹣DC=10﹣2t.
若使AEFD为菱形,则需AE=AD,
即t=10﹣2t,t= ![]() .
.
即当t= ![]() 时,四边形AEFD为菱形
时,四边形AEFD为菱形
(3)解:①∠EDF=90°时,四边形EBFD为矩形.
在Rt△AED中,∠ADE=∠C=30°,
∴AD=2AE.
即10﹣2t=2t,t= ![]() .
.
②∠DEF=90°时,由(2)四边形AEFD为平行四边形知EF∥AD,
∴∠ADE=∠DEF=90°.
∵∠A=90°﹣∠C=60°,
∴AD=AEcos60°.
即10﹣2t= ![]() t,t=4.
t,t=4.
③∠EFD=90°时,此种情况不存在.
综上所述,当t= ![]() 秒或4秒时,△DEF为直角三角形
秒或4秒时,△DEF为直角三角形
【解析】(1)在△DFC中,∠DFC=90°,∠C=30°,由已知条件求证;(2)求得四边形AEFD为平行四边形,若使AEFD为菱形则需要满足的条件及求得;(3)①∠EDF=90°时,四边形EBFD为矩形.在直角三角形AED中求得AD=2AE即求得.②∠DEF=90°时,由(2)知EF∥AD,则得∠ADE=∠DEF=90°,求得AD=AEcos60°列式得.③∠EFD=90°时,此种情况不存在.
【考点精析】关于本题考查的含30度角的直角三角形和菱形的性质,需要了解在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能得出正确答案.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】古运河是扬州的母亲河![]() 为打造古运河风光带,现有一段长为180米的河道整治任务由A、B两工程队先后接力完成
为打造古运河风光带,现有一段长为180米的河道整治任务由A、B两工程队先后接力完成![]() 工程队每天整治12米,B工程队每天整治8米,共用时20天.
工程队每天整治12米,B工程队每天整治8米,共用时20天.
![]() 根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
甲:![]() ;乙:
;乙:
根据甲、乙两名问学所列的方程组,请你分别指出未知数x、y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:x表示______,y表示______;
乙:x表示______,y表示______.
![]() 求A、B两工程队分别整治河道多少米
求A、B两工程队分别整治河道多少米![]() 写出完整的解答过程
写出完整的解答过程![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F B. BC∥EF C. ∠A=∠EDF D. AD=CF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 为
为![]() 的角平分线上的一点,点
的角平分线上的一点,点![]() 在边
在边![]() 上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边
上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边![]() 上取一点
上取一点![]() ,使得
,使得![]() ,这时他发现
,这时他发现![]() 与
与![]() 之间有一定的数量关系,请你写出
之间有一定的数量关系,请你写出![]() 与
与![]() 的数量关系__________.
的数量关系__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级(1)班共46人,前段时间有一位同学身患重病,其余同学献“爱心”为其捐款,共捐得156元,捐款情况见下表,由于记录的同学不小心,造成捐款3元和4元的人数看不清楚了.请你根据表格提供的信息,求出捐款3元和4元的人数分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图矩形ABCD中,AD=1,CD= ![]() ,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为 .
,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x﹣4与抛物线y=ax2+bx+c相交于A,B两点,其中A,B两点的横坐标分别为﹣1和﹣4,且抛物线过原点.
(1)求抛物线的解析式;
(2)在坐标轴上是否存在点C,使△ABC为等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)若点P是线段AB上不与A,B重合的动点,过点P作PE∥OA,与抛物线第三象限的部分交于一点E,过点E作EG⊥x轴于点G,交AB于点F,若S△BGF=3S△EFP , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知关于x的方程kx=11﹣2x有整数解,则负整数k的值为 .
(2)若a+b+c=0,且a>b>c,以下结论:
①a>0,c>0;
②关于x的方程ax+b+c=0的解为x=1;
③a2=(b+c)2;
④![]() 的值为0或2;
的值为0或2;
⑤在数轴上点A、B、C表示数a、b、c,若b<0,则线段AB与线段BC的大小关系是AB>BC.
其中正确的结论是 (填写正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com