
分析 (1)根据一次函数的定义,即可得出关于m的一元一次不等式以及含绝对值符号的一元一次方程,解之即可得出结论;
(2)根据一次函数图象上点的坐标特征,即可得出关于n的一元一次方程,解之即可得出结论.
解答 解(1)∵y=(m+1)x2-|m|+n+4是y关于x的一次函数,
∴m+1≠0,2-|m|=1,
解得:m=1.
∴m=1,n为任意实数.
(2)∵y=2x+n+4的图象过原点,
∴n+4=0,
解得:n=-4.
∴当m=1、n=-4时,此函数的图象经过坐标原点.
点评 本题考查了一次函数图象上点的坐标特征以及一次函数的定义,解题的关键是:(1)根据一次函数的定义,列出关于m的一元一次不等式以及含绝对值符号的一元一次方程;(2)根据一次函数图象上点的坐标特征,列出关于n的一元一次方程.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
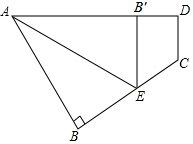 如图所示,一个四边形纸片ABCD,∠B=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕,且CD∥B′E.
如图所示,一个四边形纸片ABCD,∠B=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕,且CD∥B′E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
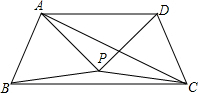 如图,△APB和△DPC是两个全等的等边三角形,AP⊥DP,有以下四个结论:①∠PBC=15°;②AC=BC;③AD∥BC;④直线PC⊥AB,其中正确的结论有①②③④(填序号).
如图,△APB和△DPC是两个全等的等边三角形,AP⊥DP,有以下四个结论:①∠PBC=15°;②AC=BC;③AD∥BC;④直线PC⊥AB,其中正确的结论有①②③④(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
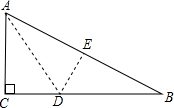 如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合.
如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
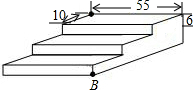 如图是一个三级台阶,它的每一级的长、宽、高分别等于55dm、10dm和6dm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物,则这只蚂蚁从A点出发沿着台阶爬到B点的最短距离是73dm.
如图是一个三级台阶,它的每一级的长、宽、高分别等于55dm、10dm和6dm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物,则这只蚂蚁从A点出发沿着台阶爬到B点的最短距离是73dm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com