
分析 (1)根据平方差公式可以解答本题;
(2)将x的值代入所求式子,然后根据平方差公式可以解答本题.
解答 解:(1)∵x1=$\sqrt{3}$+$\sqrt{2}$,x2=$\sqrt{3}$-$\sqrt{2}$,
∴x1+x2=$\sqrt{3}$+$\sqrt{2}$+$\sqrt{3}$-$\sqrt{2}$=2$\sqrt{3}$,x1-x2=($\sqrt{3}$+$\sqrt{2}$)-($\sqrt{3}$-$\sqrt{2}$)=2$\sqrt{2}$,
∴x${\;}_{1}^{2}$-x${\;}_{2}^{2}$=(x1+x2)(x1-x2)=$2\sqrt{3}×2\sqrt{2}=4\sqrt{6}$;
(2)∵x=$\sqrt{5}$-2,
∴(9+4$\sqrt{5}$)x2-($\sqrt{5}$+2)x+4
=(9+4$\sqrt{5}$)($\sqrt{5}$-2)2-($\sqrt{5}$+2)($\sqrt{5}$-2)+4
=$(9+4\sqrt{5})(9-4\sqrt{5})-1+4$
=81-80-1+4
=4.
点评 本题考查二次根式的化简求值,解答本题的关键是明确二次根式化简求值的方法.


科目:初中数学 来源: 题型:选择题
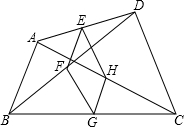 如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )
如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )| A. | AB∥DC | B. | AC=BD | C. | AC⊥BD | D. | AB=DC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
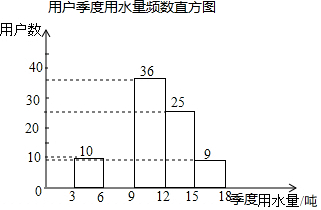 某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:
某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:| 平均用水量(吨) | 频数 | 频率 |
| 3<x≤6 | 10 | 0.1 |
| 6<x≤9 | m | 0.2 |
| 9<x≤12 | 36 | 0.36 |
| 12<x≤15 | 25 | n |
| 15<x≤18 | 9 | 0.09 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
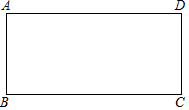 如图,在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的情况下,请补充一个条件,使四边形ABCD成为矩形,这个条件是∠A=90°.
如图,在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的情况下,请补充一个条件,使四边形ABCD成为矩形,这个条件是∠A=90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x=$\frac{1}{2}$ | B. | $\frac{x+2}{5}$=$\frac{3+x}{4}$ | C. | $\frac{1}{x}$=2 | D. | 3x-2y=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,正确结论的个数为( )
如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,正确结论的个数为( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com