
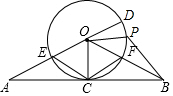
 ��ͼ���ڡ�OAB�У�OA=OB���Ե�OΪԲ�ĵġ�O����AB���е�C��ֱ��AO���O�ཻ�ڵ�E��D��OB����O�ڵ�F��P��$\widehat{DF}$���е㣬����CE��CF��BP��
��ͼ���ڡ�OAB�У�OA=OB���Ե�OΪԲ�ĵġ�O����AB���е�C��ֱ��AO���O�ཻ�ڵ�E��D��OB����O�ڵ�F��P��$\widehat{DF}$���е㣬����CE��CF��BP������ ��1���ɵ������������ߺ�һ�����ʿ�֪OC��AB�����������֪OCΪ��O�İ뾶���ʴ˿�֤��AB�ǡ�O�����ߣ�
��2���������ε����ʿ�֪��OE=EC����EOC=��COF��Ȼ��֤����OECΪ�ȱ������οɵõ���EOC�Ķ�����Ȼ�����á�DOP�Ķ��������������ڡ�OAC�У���������������Ǻ���ֵ�����OC�ij���������ݻ�����ʽ��⼴�ɣ������������ε����ʿ����OC=$\frac{\sqrt{2}}{2}$����POF=45�㣬Ȼ��ɵõ���DOP�Ķ�����������ݻ�����ʽ��⼴�ɣ�
��� �⣺��1�����ڡ�ABO�У�OA=OB��C��AB���е㣬
��OC��AB��
��OCΪ��O�İ뾶��
��AB�ǡ�O�����ߣ�
��2���١�OECFΪ���Σ�
��OE=EC����EOC=��COF��
��OE=EC=OC��
���EOC=��COF=60�㣮
���DOF=60�㣮
�֡�PΪ��DF���е㣬
���DOP=30�㣮
�ߡ�AOC=60�㣬��OCA=90�㣬
��OC=$\frac{1}{2}$OA=2��
�DP�ij�=$\frac{30��2}{180}$=$\frac{��}{3}$��
�ڡ��ı���OCBPΪ�����Σ�
���COB=��POB=45�㣮
��OC=$\frac{\sqrt{2}}{2}$OB=2$\sqrt{2}$��
��PΪ��DF���е㣬
���DOP=45�㣮
�DP�ij�=$\frac{45��2\sqrt{2}}{180}$=$\frac{\sqrt{2}��}{2}$��
�ʴ�Ϊ����$\frac{��}{3}$����$\frac{\sqrt{2}��}{2}$��
���� ������Ҫ����������ߵ��ж������ʡ����ε����ʡ������ε����ʡ�����������Ǻ������ȱ������ε����ʺ��ж��������ļ��㣬��á�DOP�Ķ����ǽ���Ĺؼ���


 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
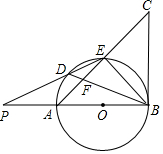 ��ͼ��AB�ǡ�O��ֱ������D��$\widehat{AE}$��һ�㣬�ҡ�BDE=��CBE��BD��AE���ڵ�F��
��ͼ��AB�ǡ�O��ֱ������D��$\widehat{AE}$��һ�㣬�ҡ�BDE=��CBE��BD��AE���ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �Ķ�����Ľ�����̣����ں����ϲ�ȫ�������̻����ݣ�
�Ķ�����Ľ�����̣����ں����ϲ�ȫ�������̻����ݣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
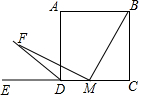 ��ͼ����������ABCD�У�AB=2����MΪ������ABCD�ı�CD�ϵĶ��㣨���C��D���غϣ�������BM����MF��BM����������ABCD����ǡ�ADE��ƽ���߽��ڵ�F����CM=x����DFM�����Ϊy����y��x֮��ĺ�����ϵʽy=-$\frac{1}{2}$x2+x��
��ͼ����������ABCD�У�AB=2����MΪ������ABCD�ı�CD�ϵĶ��㣨���C��D���غϣ�������BM����MF��BM����������ABCD����ǡ�ADE��ƽ���߽��ڵ�F����CM=x����DFM�����Ϊy����y��x֮��ĺ�����ϵʽy=-$\frac{1}{2}$x2+x���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
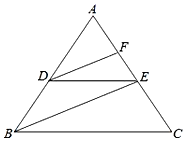
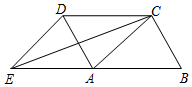 ��ͼ���ı���ABCD��ƽ���ı��Σ��ӳ�BA����E��ʹAE=AB������ED��EC��AC������һ����������ʹ�ı���ACDE��Ϊ���ε��ǣ�������
��ͼ���ı���ABCD��ƽ���ı��Σ��ӳ�BA����E��ʹAE=AB������ED��EC��AC������һ����������ʹ�ı���ACDE��Ϊ���ε��ǣ�������| A�� | AB=AD | B�� | AB=ED | C�� | CD=AE | D�� | EC=AD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com