
【题目】如图,△ABC 和△DEF 中,给出下列四组条件:

①AB=DE, BC=EF, AC=DF
②AB=DE, ∠B=∠E, BC=EF
③∠B=∠E, BC=EF, ∠C=∠F
④∠A=∠D, ∠B=∠E, AB=DF
其中能使△ABC≌△DEF 的条件有( )
A.1 组B.2 组C.3 组D.4 组
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() 的图象既是_________图形又是_________图形,它有_________条对称轴,且对称轴互相_________,对称中心是_________.
的图象既是_________图形又是_________图形,它有_________条对称轴,且对称轴互相_________,对称中心是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要在一块长52 m,宽48 m的矩形绿地上,修建同样宽的两条互相垂直的甬路,下面分别是小亮和小颖的设计方案.
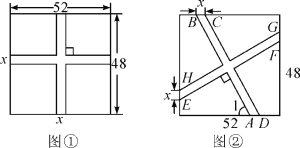
小亮设计的方案如图①所示,甬路宽度均为x m,剩余的四块绿地面积共2300 m2.
小颖设计的方案如图②所示,BC=HE=x,AB∥CD,HG∥EF,AB⊥EF,∠1=60°.
(1)求小亮设计方案中甬路的宽度x;
(2)求小颖设计方案中四块绿地的总面积.(友情提示:小颖设计方案中的x与小亮设计方案中的x取值相同)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线a、b、c上,且a、b之间的距离为1,b、c之间的距离为2,则AC2=( )

A.13B.20C.25D.26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量校园内一棵大树的高度,学校数学应用实践小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计了如图的测量方案,把镜子放在离树(AB)8.7m的点E处,然后沿直线BE后退到点D,这时恰好在镜子里看到树顶点A,再用皮尺测量得DE=2.7m,观察者眼睛距地面的高CD=1.6m,请你计算树(AB)的高度.(精确到0.1m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得到△A′B′C′,请在图中画出△A′B′C′,并写出点A′、B′、C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了庆祝校园艺术节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花一共需13元,2盆A种花和1盆B种花一共需11元.
(1)求1盆A种花和1盒B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线![]() 将这八个正方形分成面积相等的两部分,则该直线
将这八个正方形分成面积相等的两部分,则该直线![]() 的解析式为( )
的解析式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)的函数关系如图所示:
(元/千克)的函数关系如图所示:

(1)求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)求当![]() 时销售西瓜获得的利润的最大值.
时销售西瓜获得的利润的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com