
【题目】探究题:如图,在等腰三角形ABC中,AB=AC,其底边长为8 cm,腰长为5 cm,一动点P在底边上从点B出发向点C以0.25 cm/s的速度移动,请你探究:当点P运动多长时间时,点P与顶点A的连线PA与腰垂直.

【答案】当点P运动的时间为7 s或25 s时,点P与顶点A的连线与腰垂直.
【解析】
利用勾股定理求出AD的长,再利用勾股定理逆定理即可证明垂直.
(1)过点A作AD⊥BC于点D.

∵AB=AC,BC=8 cm,
∴BD=CD=![]() BC=4 cm.
BC=4 cm.
由勾股定理,得AD=![]() =3(cm).
=3(cm).
分两种情况:(1)如图,当点P运动t秒后有PA⊥AC(P在线段BD上)时,
∵AP2=PD2+AD2=PC2-AC2,
∴PD2+32=(PD+4)2-52,∴PD=2.25 cm,
∴BP=4-2.25=1.75,
∴0.25t=1.75,解得t=7.
(2)当点P运动t秒后有PA⊥AB(P在线段CD上)时,同理可得PD=2.25,∴BP=4+2.25=6.25,
∴0.25t=6.25,解得t=25.
综上所述,当点P运动的时间为7 s或25 s时,点P与顶点A的连线与腰垂直.


科目:初中数学 来源: 题型:
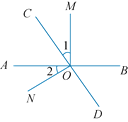
【题目】如图,直线AB,CD相交于点O,过点O作两条射线OM,ON,且∠AOM=∠CON=90°.
(1)若OC平分∠AOM,求∠AOD的度数;
(2)若∠1=∠BOC,求∠AOC和∠MOD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接五月份全县中考九年级体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表: 
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据唯一众数是13,平均数是12,那么这组数据的方差是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读新知】
三角形中任何一边的平方等于其它两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.
即:如图1,.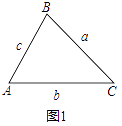
在△ABC中,已知AB=c,BC=a,CA=b,则有:
a2=b2+c2﹣2bccosA,b2=a2+c2﹣2accosB,c2=a2+b2﹣2abcosC
利用这个正确结论可求解下列问题:
例在△ABC中,已知a=2 ![]() ,b=2
,b=2 ![]() ,c=
,c= ![]() ,求∠A.
,求∠A.
解:∵a2=b2+c2﹣2bccosA,
cosA= ![]() =
= ![]() =
= ![]() .
.
∴∠A=60°.
【应用新知】
(1)选择题:在△ABC中,已知b=ccosA,a=csinB,那么△ABC是( ).
A.等边三角形
B.等腰三角形
C.等腰直角三角形
D.直角三角形
(2)如图2,
某客轮在A处看港口D在客轮的北偏东50°,A处看灯塔B在客轮的北偏西30°,距离为2 ![]() 海里,客轮由A处向正北方向航行到C处时,再看港口D在客轮的南偏东80°,距离为6海里.求此时C处到灯塔B的距离.
海里,客轮由A处向正北方向航行到C处时,再看港口D在客轮的南偏东80°,距离为6海里.求此时C处到灯塔B的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点G为BC边的中点,点H在AF上,动点P以每秒1cm的速度沿图1的边运动,运动路径为![]() ,相应的
,相应的![]() 的面积
的面积![]() 关于运动时间
关于运动时间![]() 的函数图象如图2,若
的函数图象如图2,若![]() ,则下列结论正确的个数有
,则下列结论正确的个数有![]()
![]()
![]() 图1中BC长4cm;
图1中BC长4cm;![]() 图1中DE的长是3cm;
图1中DE的长是3cm;![]() 图2中点M表示4秒时的y值为
图2中点M表示4秒时的y值为![]() ;
;![]() 图2中的点N表示12秒时y值为
图2中的点N表示12秒时y值为![]() .
.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“宜居襄阳”是我们的共同愿景,空气质量备受人们关注.我市某空气质量监测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图. 
请根据图中信息,解答下列问题:
(1)统计图共统计了天的空气质量情况;
(2)请将条形统计图补充完整;;空气质量为“优”所在扇形的圆心角度数是;
(3)从小源所在环保兴趣小组4名同学(2名男同学,2名女同学)中,随机选取两名同学去该空气质量监测站点参观,则恰好选到一名男同学和一名女同学的概率是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )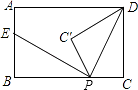
A.
B. 
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若 a、b、c 为△ABC 的三边,且满足 a2+b2+c2=ab+ac+bc.点 D 是 AC边的中点,以点 D 为顶点作∠FDE=120°,角的两边分别与直线 AB 和 BC 相交于点 F 和点 E
(1)试判断△ABC 的形状,说明理由
(2)如图 1,将△ABC 图形中∠FDE=120°绕顶点 D 旋转,当两边 DF、DE 分别与边 AB 和射线BC 相交于点 F、E 时,三线段 BE、BF、AB 之间存在什么关系?证明你的结论
(3)如图 2,当角两边 DF、DE 分别与射线 AB 和射线 BC 相交两点 F、E 时,三线段 BE、BF、AB 之间存在什么关系

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com