
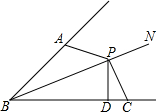
 已知如图:∠ABP=∠CBP,P为BN上一点,且PD⊥BC于点D,∠BAP+∠BCP=180°,求证:AB+BC=2BD.
已知如图:∠ABP=∠CBP,P为BN上一点,且PD⊥BC于点D,∠BAP+∠BCP=180°,求证:AB+BC=2BD. 分析 过点P作PM⊥AB,垂足为点M,首先证明PM=PD,BM=BD,根据∠BAP+∠BCP=180°,且∠BAP+∠MAP=180°,求出∠PAM=∠BCP,进而利用AAS证明△PAM≌△PCD,于是得到AM=CD,进而得出AB+BC=2BD.
解答 解:过点P作PM⊥AB,垂足为点M,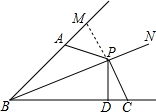
∵PM⊥AB,PD⊥BC,∠ABP=∠CBP,
∴PM=PD,BM=BD,
∵∠BAP+∠BCP=180°,且∠BAP+∠MAP=180°,
∴∠PAM=∠BCP,
在△PAM和△PCD中,
$\left\{\begin{array}{l}{∠PAM=∠PCD}\\{∠PMA=∠PDC=90°}\\{PM=PD}\end{array}\right.$,
∴△PAM≌△PCD,
∴AM=CD,
∴BM-AB=BC-BD,
∴BD-AB=BC-BD,
∴AB+BC=2BD.
点评 本题主要考查了全等三角形的判定与性质以及角平分线的性质的知识,解答本题的关键是求出∠PAM=∠BCP,利用AAS证明△PAM≌△PCD,此题难度不大.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:选择题
 如图,已知在△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,交AC边于点E,连结DE,下列五个结论:
如图,已知在△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,交AC边于点E,连结DE,下列五个结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
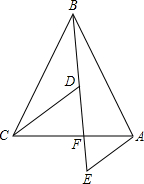 如图,在△ABC中,BC=BA,点F是AC上一点.点D是BF上一点,且∠CDF=∠CBA,AE∥CD交BF延长线于E.探究线段BD与EA的数量关系.
如图,在△ABC中,BC=BA,点F是AC上一点.点D是BF上一点,且∠CDF=∠CBA,AE∥CD交BF延长线于E.探究线段BD与EA的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 用四舍五入法对0.05049取近似值为0.050(精确到0.001) | |
| B. | 若代数式$\frac{x-2}{x+2}$有意义,则x的取值范围是x≠2且x≠-2 | |
| C. | 数据1,2,3,4的中位数是2.5 | |
| D. | 月球距离地球表面约为384000000米,将这个距离用科学记数法表示为3.84×108米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com